题目内容
 如图,E是正方形ABCD边CD的中点,F是BC边上一点,补充下列条件之一:①∠AED=∠CFE ②AE⊥FE ③BF:FC=3:1 ④AE:EF=2:1,能判定△ADE∽△EFC的个数有
如图,E是正方形ABCD边CD的中点,F是BC边上一点,补充下列条件之一:①∠AED=∠CFE ②AE⊥FE ③BF:FC=3:1 ④AE:EF=2:1,能判定△ADE∽△EFC的个数有
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:根据已知及相似三角形的判定方法对各个条件进行分析即可得到答案.
解答:∵E是正方形ABCD边CD的中点,
∴∠D=∠C=90°,
∴①∠AED=∠CFE,
∴相似;
②∵AE⊥FE,
∴∠AED+∠FEC=90°,∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∴相似;
③∵BF:FC=3:1,
∴FC:ED=EC:AD=1:2,
∴相似;
④∵AE:EF=2:1,
∴AE:EF=AD:EC=2:1,
∴相似.
故选D.
点评:此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.
分析:根据已知及相似三角形的判定方法对各个条件进行分析即可得到答案.
解答:∵E是正方形ABCD边CD的中点,
∴∠D=∠C=90°,
∴①∠AED=∠CFE,
∴相似;
②∵AE⊥FE,
∴∠AED+∠FEC=90°,∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∴相似;
③∵BF:FC=3:1,
∴FC:ED=EC:AD=1:2,
∴相似;
④∵AE:EF=2:1,
∴AE:EF=AD:EC=2:1,
∴相似.
故选D.
点评:此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )A、
| ||
B、
| ||
| C、a | ||
| D、2a |

 22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论:
22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论: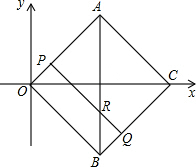 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.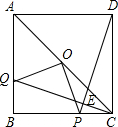 点P,连接OP,OQ;
点P,连接OP,OQ;