题目内容
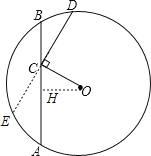
【题目】如图所示,动点C在⊙O的弦AB上运动,AB=![]() ,连接OC,CD⊥OC交⊙O于点D.则CD的最大值为 .
,连接OC,CD⊥OC交⊙O于点D.则CD的最大值为 .

【答案】![]() .
.
【解析】
试题分析:作OH⊥AB,延长DC交⊙O于E,如图,根据垂径定理得到AH=BH=![]() AB=
AB=![]() ,CD=CE,再利用相交弦定理得CDCE=BCAC,易得CD=
,CD=CE,再利用相交弦定理得CDCE=BCAC,易得CD=![]() ,当CH最小时,CD最大,C点运动到H点时,CH最小,所以CD的最大值为
,当CH最小时,CD最大,C点运动到H点时,CH最小,所以CD的最大值为![]() .
.
解:作OH⊥AB,延长DC交⊙O于E,如图,
∴AH=BH=![]() AB=
AB=![]() ,
,
∵CD⊥OC,
∴CD=CE,
∵CDCE=BCAC,
∴CD2=(BH﹣CH)(AH+CH)=(![]() ﹣CH)(
﹣CH)(![]() +CH)=3﹣CH2,
+CH)=3﹣CH2,
∴CD=![]() ,
,
∴当CH最小时,CD最大,
而C点运动到H点时,CH最小,
此时CD=![]() ,即CD的最大值为
,即CD的最大值为![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目