题目内容
如果立方体的每一个面上都有一个自然数,已知相对的两个面上两数之和都相等,若13,9,3的对面上的数分别是a,b,c,则
[(a-b)2+(b-c)2+(c-a)2]的值为
| 1 | 2 |
76
76
.分析:由已知条件相对两个面上所写的两个数之和相等得到:13+a=9+b=3+c,进一步得到a-b,b-c,c-a的值,代入即可求解.
解答:解:由题意得:13+a=9+b=3+c,
∴a-b=-4,b-c=-6,c-a=10,
∴
[(a-b)2+(b-c)2+(c-a)2]=
[(-4)2+(-6)2+102]=76.
故答案为:76.
∴a-b=-4,b-c=-6,c-a=10,
∴
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:76.
点评:本题考查了因式分解的应用,解答本题的关键是得到a-b,b-c,c-a的值后用这些式子表示出要求的原式.

练习册系列答案
相关题目
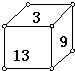 如图,立方体的每一个面上都有一个自然数,已知相对的两个面上二数之和相等.如果13,9,3的对面的数分别是a,b,c,试求a2+b2+c2-ab-bc-ca之值.
如图,立方体的每一个面上都有一个自然数,已知相对的两个面上二数之和相等.如果13,9,3的对面的数分别是a,b,c,试求a2+b2+c2-ab-bc-ca之值. 如图,立方体的每一个面上都有一个自然数,已知相对的两个面上二数之和相等.如果13,9,3的对面的数分别是a,b,c,试求a2+b2+c2-ab-bc-ca之值.
如图,立方体的每一个面上都有一个自然数,已知相对的两个面上二数之和相等.如果13,9,3的对面的数分别是a,b,c,试求a2+b2+c2-ab-bc-ca之值. [(a-b)2+(b-c)2+(c-a)2]的值为________.
[(a-b)2+(b-c)2+(c-a)2]的值为________.