题目内容

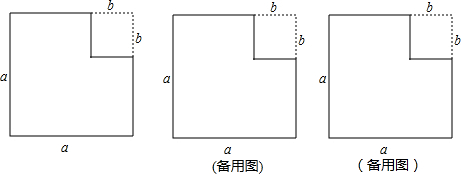
如图表示边长为a的正方形纸片剪去一个边长为b的小正方形后余下的纸片．若把余下的纸片剪开后拼成一个四边形，可以用来验证公式a²-b²=（a+b）（a-b）．
（1）请你通过对图形的剪拼，画出三种不同拼法的示意图．要求：
①拼成的图形是四边形；
②在图形上画剪切线（用虚线表示）；
③在拼出的图形上标出已知的边长．
（2）选择其中一种拼法写出验证上述公式的过程．

解：（1）如图：
①

②

③

（2）在图①中，大正方形面积为a²，小正方形面积为b²，所以阴影部分的面积为a²-b²，
在图2中，阴影部分为一长方形，长为a+b，宽为a-b，则面积为（a+b）（a-b），
由于两个阴影部分面积相等，所以有a²-b²=（a+b）（a-b）成立．
分析：（1）拼成长方形由两种，拼成等腰梯形一种；
（2）分别表示出两种情况下的面积，而面积是相等的，故可得到结果．
点评：本题考查了平方差公式几何意义的理解，将整式运算与几何图形结合，注意各个量的变化．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

用含t的代数式表示）；
（2）求点C的坐标（用含t的代数式表示）；
（3）在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求t的值．若不能，请说明理由；
（4）填空：在点P从O向A运动的过程中，点C运动路线的长为

．

（2012•义乌市模拟）如图，边长为4的等边△AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．在点P的运动过程中，线段BP的中

点为点E，将线段PE绕点P按顺时针方向旋转60°得PC．
（1）当点P运动到线段OA的中点时，点C的坐标为

；
（2）在点P从点O到点A的运动过程中，用含t的代数式表示点C的坐标；
（3）在点P从点O到点A的运动过程中，求出点C所经过的路径长．

如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
（1）当点E坐标为（3，0）时，证明CE=EP；
（2）如果将上述条件“点E坐标为（3，0）”改为“点E坐标为（t，0）”，结论CE=EP是否仍然成立，请说明理由；
（3）在y轴上是否存在点M，使得四边形BMEP是平行四边形？若存在，用t表示点M的坐标；若不存在，说明理由．

  如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA，过点P作PD⊥OB于点D．

（1）填空：PD的长为               （用含t的代数式表示）；
（2）求点C的坐标（用含t的代数式表示）；
（3）在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求t的值．若不能，请说明理由；
（4）填空：在点P从O向A运动的过程中，点C运动路线的长为

试题分类