Question

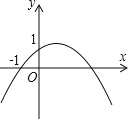
【题目】求二次函数的图象如图所示，其对称轴为直线，与轴的交点为、，其中，有下列结论：①；②；③；④；⑤；其中，正确的结论有（ ）

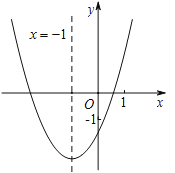
A.5B.4C.3D.2

Answer 1

【答案】C

【解析】

由抛物线开口方向得a＞0，由抛物线的对称轴为直线得＞0，由抛物线与y轴的交点位置得c＜0，则abc＜0；由于抛物线与x轴一个交点在点（0，0）与点（1，0）之间，根据抛物线的对称轴性得到抛物线与x轴另一个交点在点（-3，0）与点（-2，0）之间，即有-3＜＜-2；抛物线的对称轴为直线，且c＜-1，时，；抛物线开口向上，对称轴为直线，当时，，当得：，且，∴，即；对称轴为直线得,由于时，，则0,所以0,解得,然后利用得到.

∵抛物线开口向上，∴a＞0，

∵抛物线的对称轴为直线，∴b=2a＞0，

∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，

所以①错误；

∵抛物线与x轴一个交点在点（0，0）与点（1，0）之间，而对称轴为，由于抛物线与x轴一个交点在点（0，0）与点（1，0）之间，根据抛物线的对称轴性，∴抛物线与x轴另一个交点在点（-3，0）与点（-2，0）之间，即有-3＜＜-2，所以②正确；

∵抛物线的对称轴为直线，且c＜-1，∴当时，, 所以③正确；

∵抛物线开口向上，对称轴为直线，∴当时，，

当代入得：，

∵，∴，即,所以④错误；

∵对称轴为直线，∴,

∵由于时，，∴0,所以0,解得,

根据图象得，∴，所以⑤正确.

所以②③⑤正确, 故选：C．