题目内容
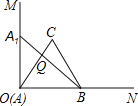
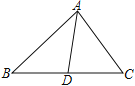
【题目】如图,![]() 中,
中,![]() ,
,![]() 是中线,
是中线,![]() ,则
,则![]() _____
_____
【答案】![]()
【解析】
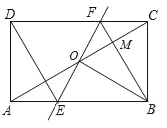
作CH⊥AD于H,延长AD到E使DE=AD=7,连接CE,作EF⊥AC于F,如图,先证明△ADB≌△EDC,得到EC=AB=10,再利用△AEF为等腰直角三角形,计算出AF=EF=![]() ,则根据勾股定理可计算出CF=
,则根据勾股定理可计算出CF=![]() ,从而得到AC=
,从而得到AC=![]() ,接着利用△ACH为等腰直角三角形,得到AH=CH=6,然后利用勾股定理计算出CD,从而得到BC的长.
,接着利用△ACH为等腰直角三角形,得到AH=CH=6,然后利用勾股定理计算出CD,从而得到BC的长.
解:作CH⊥AD于H,延长AD到E使DE=AD=7,连接CE,作EF⊥AC于F,如图,

∵AD是中线,
∴BD=CD,
在△ADB和△EDC中
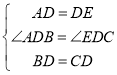 ,
,
∴△ADB≌△EDC(SAS),
∴EC=AB=10,
在RtAEF中,∵∠DAC=45°,AE=14,
∴AF=EF=![]() AE=
AE=![]() ,
,
在Rt△CEF中,![]() ,
,
∴AC=AF-CF=![]() ,
,
在Rt△ACH中,∵∠HAC=45°,
∴AH=CH=![]() AC=6,
AC=6,
∴DH=AD-AH=1,
在Rt△CDH中,CD=![]()
∴BC=2CD=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目