题目内容
阅读下列材料:
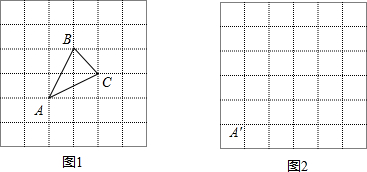
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.
数学老师给小明同学出了一道题目:在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC= ,BC=
,BC= ;
;
小明同学的做法是:由勾股定理,得AB=AC= ,BC=
,BC=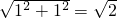 ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC.
(1)请你参考小明同学的做法,在图2正方形网格(每个小正方形边长为1)中画出格点△A′B′C′(A′点位置如图所示),使A′B′=A′C′=5,B′C′= .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
(2)观察△ABC与△A′B′C′的形状,猜想∠BAC与∠B′A′C′有怎样的数量关系,并证明你的猜想.

 解:
解:(1)正确画出△A'B'C'(画出其中一种情形即可)
(2)猜想:∠BAC=∠B'A'C'
证明:∵
 ,
, ;
;∴
 ,
,∴△ABC∽△A'B'C',
∴∠BAC=∠B'A'C'
分析:(1)读懂题意,根据勾股定理作B'C'=
 ,再以B'为顶点作A'B'=5,连接A'C'即可;
,再以B'为顶点作A'B'=5,连接A'C'即可;(2)知道两三角形三边长度,求出对应比,可看出对应成比例,所以它们相似,进而证出:∠BAC=∠B'A'C'.
点评:此题难度中等,考查相似三角形的判定和勾股定理的性质.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

 ,
,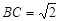 ;
; ,
, ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC. (
(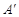 点位置如图所示),使
点位置如图所示),使 =
= =5,
=5,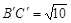 .(直接画出图形,不写过程);
.(直接画出图形,不写过程);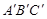 的形状,猜想∠BAC与∠
的形状,猜想∠BAC与∠ 有怎样的数量关系,并证明你的猜想.
有怎样的数量关系,并证明你的猜想. 
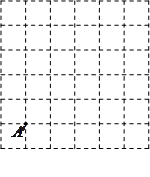
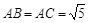 ,
,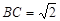 ;
;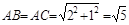 ,
,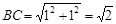 ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC.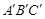 (
(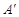 点位置如图所示),使
点位置如图所示),使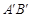 =
=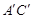 =5,
=5,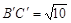 .(直接画出图形,不写过程);
.(直接画出图形,不写过程);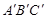 的形状,猜想∠BAC与∠
的形状,猜想∠BAC与∠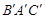 有怎样的数量关系,并证明你的猜想.
有怎样的数量关系,并证明你的猜想. 


