题目内容
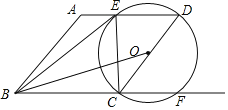
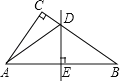
【题目】如图，在△ABC中，∠C＝90°，AB的垂直平分线分别交边BC、AB于点D、E，联结AD．
（1）如果∠CAD：∠DAB＝1：2，求∠CAD的度数；
（2）如果AC＝1，tan∠B＝
，求∠CAD的正弦值．
【答案】（1）∠CAD＝18°；（2）∠CAD的正弦值为
.
【解析】
（1）由DE垂直平分AB交边BC、AB于点D、E，可得∠DAB＝∠DBA，则∠CAD+∠DAB+∠DBA＝∠CAD+2∠DAB＝90°，而∠CAD：∠DAB＝1：2，则可求∠CAD的度数．
（2）在Rt△ABC中，AC＝1，tan∠B＝
，可求得BC，从而利用勾股定理可求得AB的值，进而可求得AE、DE的值，即可求得AD，而cos∠CAD＝
，sin∠CAD＝
，即可求∠CAD的正弦值．
（1）∵∠CAD：∠DAB＝1：2
∴∠DAB＝2∠CAD
在Rt△ABC中，∠CAD+∠DAB+∠DBA＝90°
∵DE垂直平分AB交边BC、AB于点D、E
∴∠DAB＝∠DBA
∴∠CAD+∠DAB+∠DBA＝∠CAD+2∠CAD+2∠CAD＝90°
解得，∠CAD＝18°
（2）在Rt△ABC中，AC＝1，tan∠B＝，
∴BC＝2
由勾股定理得，AB＝
∵DE垂直平分AB交边BC、AB于点D、E
∴BE＝AE＝
∵∠DAE＝∠DBE
∴在Rt△ADE中
tan∠B＝tan∠DAE＝
∴DE＝
∴由勾股定理得
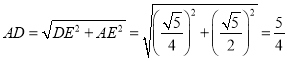∴cos∠CAD＝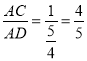
∴sin∠CAD＝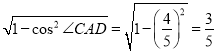
则∠CAD的正弦值为.
练习册系列答案
相关题目
