题目内容
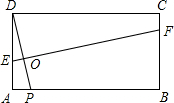
在矩形ABCD中，对角线AC、BD交于O，∠AOD=130°，则∠ACB等于
- A.65°
- B.50°
- C.40°
- D.25°
D
分析：根据矩形的性质，对角线相等且互相平分得到矩形被对角线分为4个等腰三角形，进而求得所求的角的度数．
解答：∵AD∥BC．
∴∠ACB=DAC．
∵∠AOD=130°．
∴OA=OD，△AOD是等腰三角形．
根据三角形内角和定理可得∠ACB=（180°-∠AOD）÷2=（180°-130°）÷2=25°．
故选D．
点评：本题考查矩形的性质以及三角形的内角和定理．
分析：根据矩形的性质，对角线相等且互相平分得到矩形被对角线分为4个等腰三角形，进而求得所求的角的度数．
解答：∵AD∥BC．
∴∠ACB=DAC．
∵∠AOD=130°．
∴OA=OD，△AOD是等腰三角形．
根据三角形内角和定理可得∠ACB=（180°-∠AOD）÷2=（180°-130°）÷2=25°．
故选D．
点评：本题考查矩形的性质以及三角形的内角和定理．
练习册系列答案
相关题目
，或许对你有所帮助哦！
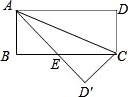如图，在矩形ABCD中，AB=5，BC=12，将矩形ABCD沿对角线对折，然后放在桌面上，折叠后所成的图形覆盖桌面的面积是
在矩形ABCD中，△ABD沿对角线BD对折，A与A′重合，AD=8，AB=6，A′D与BC相交于O．