题目内容
如图所示，在△ABC中，AC=6cm，BC=8cm，AB=10cm，D，E，F分别是AB，BC，CA的中点，则△DEF的面积为________cm2．
6
分析：根据三角形中位线的性质易得所求三角形的三边，判断出形状后可直接求得面积．
解答：∵EF，DE，DF是△ABC的中位线，
∴EF=
AB，DE=AC，DF=BC，
又∵AB=10cm，BC=8cm，AC=6cm，
∴EF=5cm，DE=3cm，DF=4cm，
而32+42=25=52，即DE2+DF2=EF2．
∴△EDF为直角三角形，
∴S△EDF=DE•DF=×3×4=6（cm2）．
故答案为6．
点评：本题考查三角形中位线等于第三边的一半的性质；要注意，根据三角形中位线定理解得所求三角形三边的长后要先判断三角形的形状，不要盲目求解．
分析：根据三角形中位线的性质易得所求三角形的三边，判断出形状后可直接求得面积．
解答：∵EF，DE，DF是△ABC的中位线，
∴EF=
AB，DE=AC，DF=BC，又∵AB=10cm，BC=8cm，AC=6cm，
∴EF=5cm，DE=3cm，DF=4cm，
而32+42=25=52，即DE2+DF2=EF2．
∴△EDF为直角三角形，
∴S△EDF=
DE•DF=×3×4=6（cm2）．故答案为6．
点评：本题考查三角形中位线等于第三边的一半的性质；要注意，根据三角形中位线定理解得所求三角形三边的长后要先判断三角形的形状，不要盲目求解．
练习册系列答案
相关题目
如图所示，在△ABC中，∠A=47°，∠C=77°，DE∥BC，BF平分∠ABC，BF交DE于点F，求∠BFE的度数．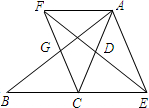
如图所示，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作AF∥BC交ED的延长线于点F，连接AE，CF．
15、如图所示，在△ABC中，DM、EN分别垂直平分AB和AC，交BC于D、E，若∠DAE=50°，则∠BAC=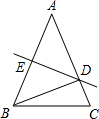
如图所示，在△ABC中，AB=AC，DE是边AB的垂直平分线，交AB于E，交AC于D，若△BCD的周长为18cm，△ABC的周长为30cm，那么BE的长为
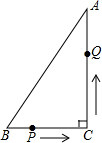如图所示，在△ABC中，BC=7cm，AB=25cm，AC=24cm，P点在BC上从B点向C点运动（不包括点C），点P的运动速度为2cm∕s；Q点在AC上从C点向点A运动（不包括点A），运动速度为5cm∕s，若点P、Q分别从B、C同时运动，请解答下面的问题，并写出主要过程．