题目内容
在同一坐标系中,若正比例函数y=2x与反比例函数y=| k-2 | x |
分析:根据正比例函数y=2x与反比例函数y=
(k≠2)的图象有公共点,则2x=
,根据一元二次方程有解,求得k的取值范围,写出一个k的值即可.
| k-2 |
| x |
| k-2 |
| x |
解答:解:∵正比例函数y=2x与反比例函数y=
(k≠2)的图象有公共点,
∴2x=
,
∴2x2-k+2=0有解,
∴△=0+8(k-2)>0,
解得k>2,
则k的一个值可以是3.
故答案为3.
| k-2 |
| x |
∴2x=
| k-2 |
| x |
∴2x2-k+2=0有解,
∴△=0+8(k-2)>0,
解得k>2,
则k的一个值可以是3.
故答案为3.
点评:本题主要考查反比例函数与一次函数的交点问题的知识点,解答本题的关键是理解两个函数图象有交点的含义,此题是开放题,k值不确定.

练习册系列答案
相关题目

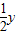 .当P点运动时,求y与x的函数关系式并写出自变量x的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中y≥0的部分有何关系?
.当P点运动时,求y与x的函数关系式并写出自变量x的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中y≥0的部分有何关系?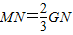 (点M、N、G按逆时针顺序),当点G在抛物线上运动时,直线AM、GH是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由.
(点M、N、G按逆时针顺序),当点G在抛物线上运动时,直线AM、GH是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由. 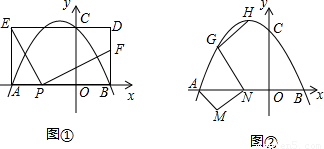
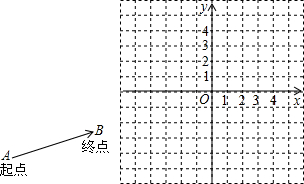
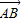 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|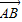 |.显然,有向线段
|.显然,有向线段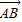 和有向线段
和有向线段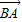 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段.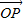 ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|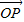 |=3.
|=3.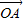 有向线段,使得
有向线段,使得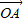 =3
=3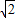 ,
,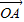 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;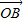 的终点B的坐标为(3,
的终点B的坐标为(3,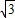 ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角;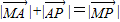 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)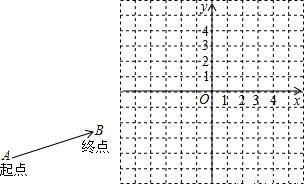
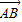 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|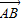 |.显然,有向线段
|.显然,有向线段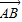 和有向线段
和有向线段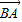 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段.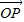 ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|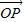 |=3.
|=3. 有向线段,使得
有向线段,使得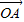 =3
=3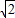 ,
,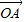 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;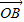 的终点B的坐标为(3,
的终点B的坐标为(3,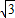 ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角;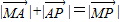 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)