题目内容
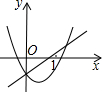
如图，坐标系的原点为O，点P是第一象限内抛物线y=
x2-1上的任意一点，PA⊥x轴于点A．则OP-PA值为（ ）
| 1 |
| 4 |
| A．1 | B．2 | C．3 | D．4 |
设P点坐标为（a，
a2-1），则OA=a，PA=
a2-1，
∴OP=
=
=
a2+1，
∴OP-PA=
a2+1-（
a2-1）=2．
故选B．
| 1 |
| 4 |
| 1 |
| 4 |
∴OP=
a2+(
|
(
|
| 1 |
| 4 |
∴OP-PA=
| 1 |
| 4 |
| 1 |
| 4 |
故选B．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
与x轴正半轴交于点A（3，0）.以OA为边在x轴上方作正方形OABC，延长CB交抛物线于点D，再以BD为边向上作正方形BDEF.
