题目内容
如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为（ ）
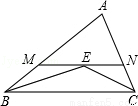
A. 6 B. 7 C. 8 D. 9
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
新课标阶梯阅读训练系列答案口算心算速算应用题系列答案题目内容
如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为（ ）
A. 6 B. 7 C. 8 D. 9
新课标阶梯阅读训练系列答案口算心算速算应用题系列答案
的相反数是____________.
B. 
C. 5 D. 6
．其中正确的结论有（ ）
， 
，0，﹣π， 
， 
，0.1010010001…（相连两个1之间依次多一个 0），其中无理数有（ ）个．
，