Question

【题目】在菱形ABCD中，的两边分别与AB，BC交于点E，F，与对角线AC交于点G，H，已知，．

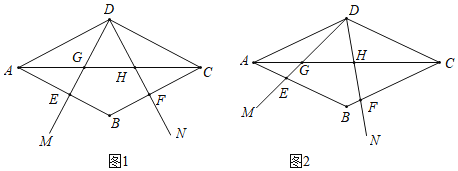
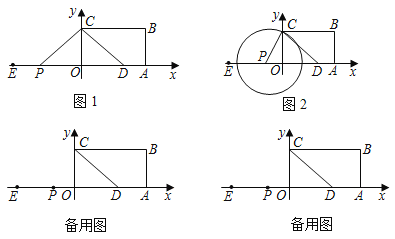
（1）如图1，当，时，

①求证：；

②求线段GH的长；

（2）如图2，当绕点D旋转时，线段AG，GH，HC的长度都在变化．设线段，，，试探究p与mn的等量关系，并说明理由．

Answer 1

【答案】（1）①详见解析；②2；（2）

【解析】

（1）①利用AAS直接得出结论；

②先判断出，，证明是等边三角形，进而求出，即可得出结论；

（2）先判断出C'G＝CH＝p，再求出AP＝m，PG＝m，进而得出PC'＝nm，进而得出p2＝（nm）2＋（m）2①，再判断出m＋n＋p＝6②，联立即可得出结论．

（1）①证明：∵，，

∴

∵在菱形ABCD中，，，

∴；

②解：∵在菱形ABCD中，，，，

∴，，

∵，

∴，

∴，/span>

∴，

同理，

∵，，

∵

∴是等边三角形，即，

∴，

∴；

（2）解：p与mn的等量关系是：．

理由：将绕点D顺时针旋转得到，则，，，，

连接KG，作于点R，

则，

，

∴，

又∵，，

∴，

∴，

∵在中，，

∴，，

∴，

∴在中，，即，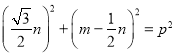

整理得：，

又∵，

∴，

∴，化简得．

因此所求的等量关系式是：．