题目内容
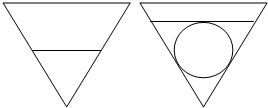 如图:有一轴截面为正三角形的圆锥形容器,内部盛水高度为10cm,放入一个球后,水面恰好与球相切,求球的半径.(圆锥的体积公式V=
如图:有一轴截面为正三角形的圆锥形容器,内部盛水高度为10cm,放入一个球后,水面恰好与球相切,求球的半径.(圆锥的体积公式V=| 1 |
| 3 |
| 4 |
| 3 |
分析:根据水的高度以及圆锥形容器的轴截面为等边三角形得到水的体积,设出球的半径表示出球的体积,则根据放球后总体积V′=V球+V水,得到关于铁球R的方程,解方程即可.
解答:解:如图所示,则△ABS为等边三角形,
∵SG=h=10,DG=
×10=
,
∴V水=
•DG2•SG=
h3.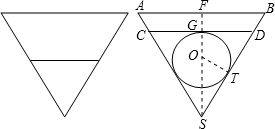
设铁球的半径为R,
则SO=2R,SG=3R,
在Rt△FSB中,DG=SGtan∠FSB=
R,
设放入球之后,球与水共占体积为V′,
则V′=
•(DG)2•SG=
(
R)2•3R=3πR3,V球=
R3.
依题意,有V′=V球+V水,
即3πR3=
πR3+
h3,
∴R=
×10=
,
答:铁球的半径为
.
∵SG=h=10,DG=
| ||
| 3 |
10
| ||
| 3 |
∴V水=
| π |
| 3 |
| π |
| 9 |

设铁球的半径为R,
则SO=2R,SG=3R,
在Rt△FSB中,DG=SGtan∠FSB=
| 3 |
设放入球之后,球与水共占体积为V′,
则V′=
| π |
| 3 |
| π |
| 3 |
| 3 |
| 4π |
| 3 |
依题意,有V′=V球+V水,
即3πR3=
| 4 |
| 3 |
| π |
| 9 |
∴R=
| |||
| 15 |
2
| |||
| 3 |
答:铁球的半径为
2
| |||
| 3 |
点评:本题考查了切线的性质、等边三角形的性质、圆锥的体积公式、球的体积的求法,属于中档题目,也重点考查学生的计算能力.

练习册系列答案
相关题目
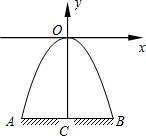 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求: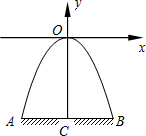 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求: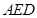 和矩形
和矩形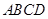 构成,矩形的长
构成,矩形的长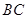 为
为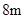 ,宽
,宽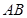 为
为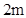 ,以
,以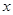 轴,线段
轴,线段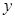 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,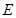 到坐标原点
到坐标原点 的距离为
的距离为 .
. (2)一辆货运卡车高
(2)一辆货运卡车高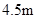 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?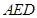 和矩形
和矩形 构成,矩形的长
构成,矩形的长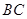 为
为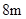 ,宽
,宽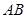 为
为 ,以
,以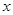 轴,线段
轴,线段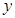 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,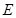 到坐标原点
到坐标原点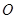 的距离为
的距离为 .
. (2)一辆货运卡车高
(2)一辆货运卡车高 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?