Question

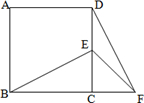如图，已知，正方形ABCD中，E是CD边上的一点，F为BC延长线上一点，CE=CF．
（1）求证：△BEC≌△DFC；
（2）若BC+DF=9，CF=3，求正方形ABCD的面积．

Answer 1

分析：（1）正方形的四个边相等，四个角都是直角，因此可得到BC=DC，∠ECD=∠FCD，从而可证明三角形全等．
（2）设BC=x，则CD=x，DF=9-x，CF=4，可用勾股定理求出x，因此可求出正方形ABCD的面积．

解答：（1）证明：在△BCE和△DCF中，

BC=CD ∠BCE=∠DCF CE=CF

，
∴△BEC≌△DFC（SAS）；

（2）解：设BC=x，则CD=x，DF=9-x，
在Rt△DCF中，CF=3，
∴CF²+CD²=DF²，
3²+x²=（9-x）²，
解得x=4，正方形的面积为：4×4=16．

点评：本题考查正方形的性质，正方形的四个角都是直角，四个边相等，以及全等三角形的判定定理和性质，以及勾股定理．