题目内容
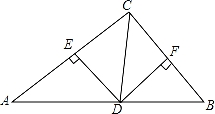
如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
4 .
【考点】角平分线的性质.
【专题】压轴题.
【分析】首先根据CD平分∠ACB交AB于点D,可得∠DCE=∠DCF;再根据DE⊥AC,DF⊥BC,可得∠DEC=∠DFC=90°,然后根据全等三角形的判定方法,判断出△CED≌△CFD,即可判断出DF=DE;最后根据三角形的面积=底×高÷2,求出△BCD的面积是多少即可.
【解答】解:∵CD平分∠ACB交AB于点D,
∴∠DCE=∠DCF,
∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°,
在△DEC和△DFC中,
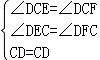 (AAS)
(AAS)
∴△DEC≌△DFC,
∴DF=DE=2,
∴S△BCD=BC×DF÷2
=4×2÷2
=4
答:△BCD的面积是4.
故答案为:4.
【点评】(1)此题主要考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:角的平分线上的点到角的两边的距离相等.
(2)此题还考查了全等三角形的判定和性质的应用,以及三角形的面积的求法,要熟练掌握.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 ,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
 = .
= .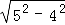 =1×3;②
=1×3;②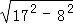 =3×5;③
=3×5;③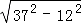 =5×7;
=5×7;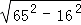 = × ;
= × ;