Question

【题目】抛物线y=﹣x2+4ax+b（a＞0）与x轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．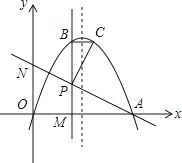

（1）a= 时，求抛物线的解析式和BC的长；
（2）如图a＞1时，若AP⊥PC，求a的值．

Answer 1

【答案】
（1）

解：∵抛物线y=﹣x2+4ax+b（a＞0）经过原点O，

∴b=0，

∵a= ，

∴抛物线解析式为y=﹣x2+6x，

∵x=2时，y=8，

∴点B坐标（2，8），

∵对称轴x=3，B、C关于对称轴对称，

∴点C坐标（4，8），

∴BC=2．

（2）

解：

∵AP⊥PC，

∴∠APC=90°，

∵∠CPB+∠APM=90°，∠APM+∠PAM=90°，

∴∠CPB=∠PAM，

∵∠PBC=∠PMA=90°，

∴△PCB∽△APM，

∴ ，

∴ ，

整理得a2﹣4a+2=0，解得a=2± ，

∵a＞0，

∴a=2+ ．

【解析】（1）根据抛物线经过原点b=0，把a= 、b=0代入抛物线解析式，即可求出抛物线解析式，再求出B、C坐标，即可求出BC长．（2）利用△PCB∽△APM，得 = ，列出方程即可解决问题．本题考查二次函数性质、相似三角形的判定和性质、待定系数法等知识，解题的关键是利用相似三角形性质列出方程解决问题，学会转化的思想，属于中考常考题型．
【考点精析】掌握二次函数的性质和轴对称的性质是解答本题的根本，需要知道增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；关于某条直线对称的两个图形是全等形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上．