Question

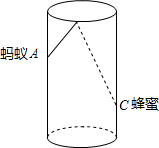如图，圆柱形纸杯高8cm，底面周长为l2，cm，在纸杯内壁离杯底2Cem的点C处有一滴蜂蜜，一只蚂蚁正好在纸杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为（　　）

• A、2

  3

• B、6

  2

• C、10
• D、以上答案都不对

Answer 1

分析：将杯子侧面展开，建立A关于EF的对称点A′，根据两点之间线段最短可知A′C的长度即为所求．

解答：解：如图：
将杯子侧面展开，作A关于EF的对称点A′，
连接A′C，则A′C即为最短距离，
由题意可得出：A′D=6cm，CD=8cm，
A′C=

A′D2+CD2

=10（cm），
故选：C．

点评：本题考查了平面展开---最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．