题目内容
Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB与DE重合.
1.求证:四边形ABFC为平行四边形
2.取BC中点O,将△ABC绕点O顺时针方向旋转到如图(二)中△![]() 位置,直线
位置,直线![]() 与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
3.在(2)的条件下,指出当旋转角为多少度时,四边形PCQB为菱形(不要求证明).
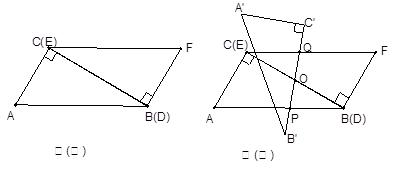
1.![]() ……………………1分
……………………1分
∴AB=CF,AC=BF ……………………2分
∴四边形ABCF为平行四边形 ……………………3分
(用其它判定方法也可)
2.OP=OQ ……………………4分理由如下:![]()
![]() ……………………7分
……………………7分
∴OP=OQ ……………………9分
(用平行四边形对称性证明也可)
3.90o ……………………10分
解析:(1)已知△ABC≌△FCB,根据全等三角形的性质可知AB=CF,AC=BF,根据两组对边分别相等的四边形是平行四边形即可得到结论.
(2)根据已知利用AAS判定△COQ≌△BOP,根据全等三角形的性质即可得到OP=OQ.
(3)根据对角线互相垂直的平行四边形的菱形进行分析即可.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
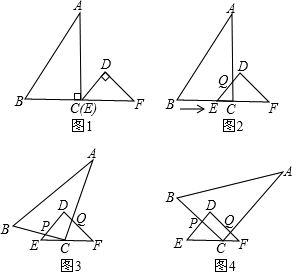 已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.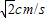 ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转;
 ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转;
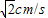 ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转;
 ,当QC⊥DF时暂停旋转;
,当QC⊥DF时暂停旋转;