题目内容
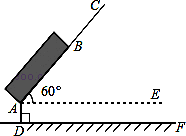
一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据: )
)
【考点】解直角三角形的应用.
【分析】作CG⊥AE于点G,在直角△ACG中利用三角函数即可求得CG的长,再加上AD的长度即可求解.
【解答】解:作CG⊥AE于点G.
在直角△ACG中,AC=AB+BC=50+30=80cm.
sin∠CAG= ,
,
∴CG=AC•sin∠CAG=80× =40
=40 ≈69.2(cm).
≈69.2(cm).
则拉杆把手处C到地面的距离是:69.2+8=77.2≈77cm.

【点评】此题考查了三角函数的基本概念,主要是正弦概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 B.
B. C.
C. D.
D.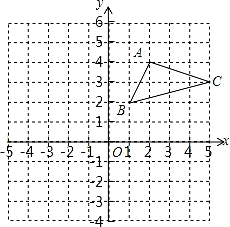
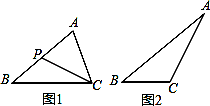

 的大正方形中有一个边长为
的大正方形中有一个边长为 的小正方形,请你写出阴影部分面积是______________(写成两数平方差的形式)
的小正方形,请你写出阴影部分面积是______________(写成两数平方差的形式)