题目内容
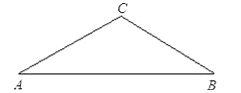
【题目】如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
【答案】(1)作图见解析;(2)证明见解析.
【解析】
试题分析:(1)由已知得到△ACD是直角三角形,那么过A,D,C三点作⊙O,根据圆周角是直角所对的弦是直径得,AD为⊙O的直径,所以作AD的中点O即为圆心,再以点O为圆心,OA长为半径即可作出⊙O.
(2)先连接OC,已知已知在等腰△ABC中,∠A=∠B=30°,能求出∠ACB=120°,在⊙O中OA=OC,得到,∠ACO=∠A=30°,那么∠BCO=∠ACB﹣∠ACO=120°﹣30°=90°,从而推出BC是过A,D,C三点的圆的切线.
试题解析:(1)作出圆心O,以点O为圆心,OA长为半径作圆;
(2)证明:∵CD⊥AC,∴∠ACD=90°,∴AD是⊙O的直径
连接OC,∵∠A=∠B=30°,∴∠ACB=120°,又∵OA=OC,∴∠ACO=∠A=30°,∴∠BCO=∠ACB﹣∠ACO=120°﹣30°=90°,∴BC⊥OC,∴BC是⊙O的切线.


练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目