题目内容
等腰三角形一腰上的中线分此三角形为两个三角形，若这两个三角形的周长相差2，且等腰三角形底边长是4，则它的腰长是（ ）
| A．3或5 | B．6 | C．4或6 | D．2或6 |
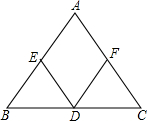
如图，BC=4，
由题意一腰上的中线把三角形周长分成两部分的差为2，
所以AC+AD-BD-BC=2，即AC=6，
也有可能是BD+BC-AC-AD=2，解得AC=2，
故选D．
由题意一腰上的中线把三角形周长分成两部分的差为2，
所以AC+AD-BD-BC=2，即AC=6，
也有可能是BD+BC-AC-AD=2，解得AC=2，
故选D．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
