题目内容
解方程组  .
.
解:设 ,
,
则原方程组可化为
解此方程得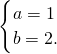
∴
∴
检验:将 代入(2x-y)=
代入(2x-y)= ≠0.
≠0.
∴所以原方程组的解是
分析:观察分式方程中发现,可设 ,
, ,将原方程组转换成整式方程组,求出a、b的值,然后再求x、y的值.
,将原方程组转换成整式方程组,求出a、b的值,然后再求x、y的值.
点评:本题主要考查解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,
解分式方程一定注意要验根.
 ,
,
则原方程组可化为

解此方程得
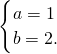
∴

∴

检验:将
 代入(2x-y)=
代入(2x-y)= ≠0.
≠0.∴所以原方程组的解是

分析:观察分式方程中发现,可设
 ,
, ,将原方程组转换成整式方程组,求出a、b的值,然后再求x、y的值.
,将原方程组转换成整式方程组,求出a、b的值,然后再求x、y的值.点评:本题主要考查解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,
解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)解方程组:
(1)解方程组: