Question

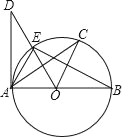
【题目】四边形ABCD中，∠ABC+∠D＝180°，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F．

（1）求证：△CBE≌△CDF；

（2）若AB＝3，DF＝2，求AF的长．

Answer 1

【答案】（1）详见解析；（2）5．

【解析】

（1）根据角平分线的性质可得到CE＝CF，根据余角的性质可得到∠EBC＝∠D，已知CE⊥AB，CF⊥AD，从而利用AAS即可判定△CBE≌△CDF．

（2）已知EC＝CF，AC＝AC，则根据HL判定△ACE≌△ACF得AE＝AF，最后证得AB+DF＝AF即可．

（1）证明：∵AC平分∠BAD，CE⊥AB，CF⊥AD

∴CE＝CF

∵∠ABC+∠D＝180°，∠ABC+∠EBC＝180°

∴∠EBC＝∠D．

在△CBE与△CDF中，

，

∴△CBE≌△CDF（AAS）；

（2）在Rt△ACE与Rt△ACF中，

，

∴Rt△ACE≌Rt△ACF（HL），

∴AE＝AF，

∴AB+DF＝AB+BE＝AE＝AF，

∵AB＝3，DF＝2，

∴AF＝3+2＝5．