题目内容
在同一直角坐标平面内直线y=k1x与双曲线y=| k2 | x |
分析：若两函数图象没有交点，则图象位于不同的象限，即k1k2＜0．
解答：解：因为在同一直角坐标平面内直线y=k1x与双曲线y=
没有交点，
所以当k2＞0，直线y=k1x的图象经过二、四象限和原点，
而当k2＞0，双曲线y=
的图象分布在一、三象限，两条函数没有交点，
则说明当k1＞0时，则k2＜0．
同样也可得到当k1＜0时，则k2＞0，
也就是k1k2必然异号，即k1k2＜0．
| k2 |
| x |
所以当k2＞0，直线y=k1x的图象经过二、四象限和原点，
而当k2＞0，双曲线y=
| k2 |
| x |
则说明当k1＞0时，则k2＜0．
同样也可得到当k1＜0时，则k2＞0，
也就是k1k2必然异号，即k1k2＜0．
点评：利用函数图象的规律，先求出k1，k2的取值范围，再求出k1k2的取值范围，运用了数形结合的思想．
练习册系列答案
相关题目
在同一直角坐标平面内，如果直线y=k1x与双曲线y=
没有交点，那么k1和k2的关系一定是（ ）
| k2 |
| x |
| A、k1、k2异号 |
| B、k1、k2同号 |
| C、k1＞0，k2＜0 |
| D、k1＜0，k2＞0 |
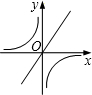
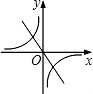
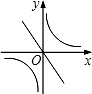
没有交点，那么k1和k2的关系一定是（ ）