题目内容
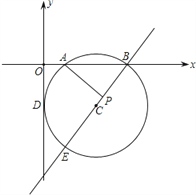
【题目】如图，在平面直角坐标系xOy中，动点A(a,0)在x轴的正半轴上，定点B(m, n)在第一象限内（m＜2≤a）.在△OAB外作正方形ABCD和正方形OBEF ， 连接FD ， 点M为线段FD的中点.作BB1⊥x轴于点B1 ， 作FF1⊥x轴于点F1.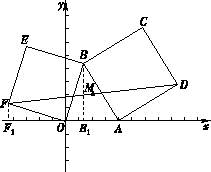
（1）填空：由△≌△ ， 及B(m, n)可得点F的坐标为 ， 同理可得点D的坐标为；（说明：点F ， 点D的坐标用含m ， n ， a的式子表示）
（2）直接利用（1）的结论解决下列问题：
①当点A在x轴的正半轴上指定范围内运动时，点M总落在一个函数图象上，求该函数的解析式（不必写出自变量x的取值范围）；
②当点A在x轴的正半轴上运动且满足2≤a≤8时，求点M所经过的路径的长.
【答案】
（1）
；
；
；
（2）
解：①设点M的坐标为 
.
∵ 点M为线段FD的中点， 
， 
，
可得点M的坐标为 
.
∴ 
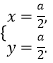
消去a，得 
.
所以，当点A在x轴的正半轴上指定范围内运动时，相应的点M在运动时总落在直线 上，即点M总落在函数 的图象上.
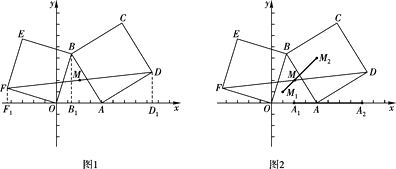
②如图2，当点A在x轴的正半轴上运动且满足2≤a≤8时，点A运动的路径为线段 
，其中 
， 
，相应地，点M所经过的路径为直线 上的一条线段 
，其中 
， 
.
而 
，
∴ 点M所经过的路径的长为 
【解析】（1）如图1.由△ 
≌△ 
，及B(m, n)可得点F的坐标为 
，同理可得点D的坐标为 
.
【考点精析】根据题目的已知条件，利用线段的中点和两点间的距离的相关知识可以得到问题的答案，需要掌握线段的中点到两端点的距离相等；同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
