题目内容
 如图,抛物线y=x2-2x+
如图,抛物线y=x2-2x+ 与y轴交于点C,与x轴交于点A、B(B点在A点的右侧).若点P是抛物线对称轴上的一动点,则△OCP的面积为________;若点P(1,a)是抛物线对称轴上的一动点,且满足△PBC的面积为2,则a的值为________.
与y轴交于点C,与x轴交于点A、B(B点在A点的右侧).若点P是抛物线对称轴上的一动点,则△OCP的面积为________;若点P(1,a)是抛物线对称轴上的一动点,且满足△PBC的面积为2,则a的值为________.

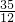 ,
,
分析:根据抛物线的对称轴,可得出△OCP的边OC上的高,继而可计算△OCP的面积;由B、C坐标求出直线BC解析式,设BC与抛物线交点为D,用含a的式子表示出DP,根据S△PBC=S△PDC+S△PDB,可得出关于a的方程,解出即可.
解答:
 解:∵抛物线解析式为y=x2-2x+
解:∵抛物线解析式为y=x2-2x+ ,
,∴抛物线对称轴为直线x=1,点C的坐标为(0,
 ),
),∴S△OCP=
 ×
× ×1=
×1= ;
;令x2-2x+
 =0,
=0,解得:x1=
 ,x2=
,x2= ,
,故点A的坐标为(
 ,0),点B的坐标为(
,0),点B的坐标为( ,0),
,0),设直线BC与抛物线对称轴交于点D,其解析式为y=kx+b,
将点B、点C坐标代入可得:
 ,
,解得:
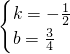 ,
,故直线BC的解析式为y=-
 x+
x+ ,
,则点D的坐标为(1,
 ),PD=|a-
),PD=|a- |,
|,则S△PBC=S△PDC+S△PDB=
 PD×OM+
PD×OM+ PD×BM=
PD×BM= PD×OB=
PD×OB= |a-
|a- |×
|× =2,
=2,解得:a=
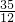 或a=-
或a=- .
.故答案为:
 ,
,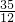 、-
、- .
.点评:本题考查了二次函数的综合,涉及了待定系数法求一次函数解析式、抛物线与x轴的交点及三角形的面积,最后一空的关键是用含a的式子表示出△PBC的面积,难度较大.

练习册系列答案
相关题目
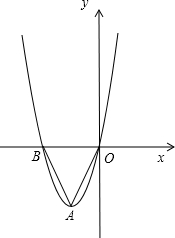 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO. 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l. (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.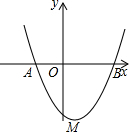 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.