题目内容
若两圆半径分别为R和r（R＞r），圆心距为d，且R2+d2=r2+2Rd，则两圆的位置关系为（ ）
分析：先利用分解因式，得到关于R、d、r之间的关系，再根据圆心距与两圆半径的关系进行解答．
解答：解：∵R2+d2=r2+2Rd，
R2+d2-2Rd=r2，
∴（R-d）2=r2，
解得，R-d=±r，
∴①当R-r=d时，两圆内切，
②当R-d=-r时，即R+r=d，两圆外切．
∴两圆的位置关系是内切或外切．
故选B．
R2+d2-2Rd=r2，
∴（R-d）2=r2，
解得，R-d=±r，
∴①当R-r=d时，两圆内切，
②当R-d=-r时，即R+r=d，两圆外切．
∴两圆的位置关系是内切或外切．
故选B．
点评：本题利用了两圆外切时，圆心距等于两圆半径之和，两圆内切时，圆心距等于两圆半径之差；熟练掌握此关系是解本题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
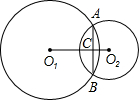已知：如图，⊙O1与⊙O2相交于A、B，若两圆半径分别为12和5，O1O2=13，则AB=