题目内容
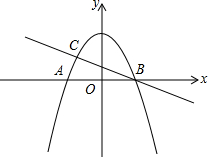 抛物线y=-
抛物线y=-| 3 |
| 4 |
| 3 |
| 4 |
(1)写出直线BC的解析式;
(2)求S△ABC.
考点:抛物线与x轴的交点,待定系数法求一次函数解析式
专题:
分析:(1)由抛物线的解析式可求出A,B的坐标,进而可求出直线BC的解析式;
(2)由(1)可知AB的长,再求出C点的纵坐标即可得到AB边上的高线,利用三角形的面积公式计算即可得到问题答案.
(2)由(1)可知AB的长,再求出C点的纵坐标即可得到AB边上的高线,利用三角形的面积公式计算即可得到问题答案.
解答:解:(1)∵抛物线y=-
x2+3与x轴交于A、B两点,
∴A的坐标(-2,0),B的坐标(2,0),
∵直线y=-
x+b过B点,
∴0=-
×2+b,
∴b=
,
∴直线BC的解析式是y=-
x+
;
(2)∵A的坐标(-2,0),B的坐标(2,0),
∴AB=4,
∵抛物线y=-
x2+3与直线y=-
x+
相交于B、C两点,
∴
,
∴C的坐标(-1,
),
∴求S△ABC=
×4×
=1.
| 3 |
| 4 |
∴A的坐标(-2,0),B的坐标(2,0),
∵直线y=-
| 3 |
| 4 |
∴0=-
| 3 |
| 4 |

∴b=
| 3 |
| 2 |
∴直线BC的解析式是y=-
| 3 |
| 4 |
| 3 |
| 2 |
(2)∵A的坐标(-2,0),B的坐标(2,0),
∴AB=4,
∵抛物线y=-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
∴
|
∴C的坐标(-1,
| 1 |
| 2 |
∴求S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了抛物线与x轴的交点以及二次函数的性质,得出各点的坐标是解答本题的突破口,另外注意将不规则图形的面积转化为几个规则图形的面积和进行求解.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
(-
)×(-0.25)×(-4)×(+1
)=[(-
)×(+1
)]×[(-0.25)×(-4)]这是为了运算简便而使用( )
| 7 |
| 8 |
| 1 |
| 7 |
| 7 |
| 8 |
| 1 |
| 7 |
| A、乘法交换律 |
| B、乘法结合律 |
| C、乘法分配律 |
| D、乘法结合律和交换律 |
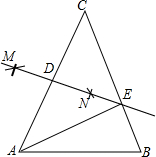 如图,在△ABC中,AC=BC,AB+BC=20,分别以点A、C为圆心,大于
如图,在△ABC中,AC=BC,AB+BC=20,分别以点A、C为圆心,大于 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB,垂足为E,CD=2cm,则△DEB的周长为
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB,垂足为E,CD=2cm,则△DEB的周长为