题目内容
如图,等腰△ABC中,AB=AC=13,BC=10,以AC为直径作⊙O交BC于点D,交AB于点G,过点D作⊙O的切线交AB于点E,交 AC的延长线与点F.
AC的延长线与点F.
(1)求证:EF⊥AB;
(2)求cos∠F的值.
证明:(1)连接OD,

∵OC=OD,
∴∠ODC=∠OCD,
又∵AB=AC,
∴∠OCD=∠B,
∴∠ODC=∠B,
∴OD∥AB,
∵ED是⊙O的切线,OD是⊙O的半径,
∴OD⊥EF,
∴AB⊥EF;
(2)连接AD、CG,
∵AD是⊙O的直径,
∴∠ADC=∠AGC=90°,
∵AB⊥EF,
∴DE∥CG,
∴∠F=∠GCA,
∵AB=AC,
∴DC= BC=5,
BC=5,
Rt△ADC中,AD= =12,
=12,
∵S△ABC= AD•BC=
AD•BC= AB•CG,
AB•CG,
∴CG= =
=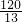 ,
,
在Rt△CGA中,cos∠GCA= =
= ,
,
∴cos∠F= .
.
分析:(1)连接OD,由EF为圆O的切线,利用切线的性质得到OD与EF垂直,又OD=OC,利用等边对等角得到一对角相等,再由AB=AC,根据等边对等角得到另一对角相等,等量代换可得出一对同位角相等,根据同位角相等两直线平行可得出OD与AB平行,由与平行线中的一条直线垂直,与另一条也垂直,即可得证;
(2)连接AD,CG,由AC为圆O的直径,根据直径所对的圆周角为直角,可得出∠ADC与∠AGC都为直角,又FE垂直与AB,且CG垂直与AB,可得出GC与EF平行,根据两直线平行同位角相等可得出∠F=∠ACG,由AB=AC,AD垂直与BC,根据三线合一得到D为BC的中点,由BC的长求出DC的长,在直角三角形ADC中,由DC及AC的长,利用勾股定理求出AD的长,再根据三角形ABC的面积由AD与BC乘积的一半来求,也可以由AB与CG乘积的一半来求出,两者相等可得出GC的长,由∠ACG的邻边GC与斜边AC的比值求出cos∠ACG的值,即为cos∠F的值.
点评:此题考查了切线的性质,勾股定理,平行线的判定与性质,圆周角定理,锐角三角函数定义,以及等腰三角形的性质,熟练掌握性质及定理是解本题的关键.

∵OC=OD,
∴∠ODC=∠OCD,
又∵AB=AC,
∴∠OCD=∠B,
∴∠ODC=∠B,
∴OD∥AB,
∵ED是⊙O的切线,OD是⊙O的半径,
∴OD⊥EF,
∴AB⊥EF;
(2)连接AD、CG,
∵AD是⊙O的直径,
∴∠ADC=∠AGC=90°,
∵AB⊥EF,
∴DE∥CG,
∴∠F=∠GCA,
∵AB=AC,
∴DC=
 BC=5,
BC=5,Rt△ADC中,AD=
 =12,
=12,∵S△ABC=
 AD•BC=
AD•BC= AB•CG,
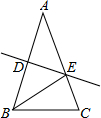
AB•CG,∴CG=
 =
=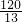 ,
,在Rt△CGA中,cos∠GCA=
 =
= ,
,∴cos∠F=
 .
.分析:(1)连接OD,由EF为圆O的切线,利用切线的性质得到OD与EF垂直,又OD=OC,利用等边对等角得到一对角相等,再由AB=AC,根据等边对等角得到另一对角相等,等量代换可得出一对同位角相等,根据同位角相等两直线平行可得出OD与AB平行,由与平行线中的一条直线垂直,与另一条也垂直,即可得证;
(2)连接AD,CG,由AC为圆O的直径,根据直径所对的圆周角为直角,可得出∠ADC与∠AGC都为直角,又FE垂直与AB,且CG垂直与AB,可得出GC与EF平行,根据两直线平行同位角相等可得出∠F=∠ACG,由AB=AC,AD垂直与BC,根据三线合一得到D为BC的中点,由BC的长求出DC的长,在直角三角形ADC中,由DC及AC的长,利用勾股定理求出AD的长,再根据三角形ABC的面积由AD与BC乘积的一半来求,也可以由AB与CG乘积的一半来求出,两者相等可得出GC的长,由∠ACG的邻边GC与斜边AC的比值求出cos∠ACG的值,即为cos∠F的值.
点评:此题考查了切线的性质,勾股定理,平行线的判定与性质,圆周角定理,锐角三角函数定义,以及等腰三角形的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、80° | B、70° | C、60° | D、50° |
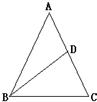 13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为
13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为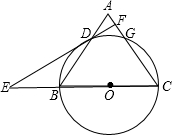 如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=
如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE= 如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点.
如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点. 如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.
如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.