题目内容
一种盛饮料的圆柱形杯，测得内部底面半径为2.5cm，高为12cm，吸管最大程度倾斜放进杯里，杯口外面至少要露出4.6cm，则吸管至少要________cm．
17.6
分析：由于吸管、圆柱形杯内部底面直径与杯壁正好构成直角三角形，故可先利用勾股定理求出AB的长，进而可得出结论．
解答：
解：如图所示：
∵杯子底面半径为2.5cm，高为12cm，
∴BC=2×2.5=5cm，AC=12cm，
∵吸管、圆柱形杯内部底面直径与杯壁正好构成直角三角形，
∴AB=
=
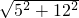=13cm，
∵杯口外面至少要露出4.6cm，
∴吸管的长至少为：13+4.6=17.6cm．
故答案为：17.6．
点评：本题考查的是勾股定理在实际生活中的运用，解答此类题目的关键是构造出直角三角形，再利用勾股定理解答．
分析：由于吸管、圆柱形杯内部底面直径与杯壁正好构成直角三角形，故可先利用勾股定理求出AB的长，进而可得出结论．
解答：
解：如图所示：∵杯子底面半径为2.5cm，高为12cm，
∴BC=2×2.5=5cm，AC=12cm，
∵吸管、圆柱形杯内部底面直径与杯壁正好构成直角三角形，
∴AB=
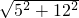==13cm，∵杯口外面至少要露出4.6cm，
∴吸管的长至少为：13+4.6=17.6cm．
故答案为：17.6．
点评：本题考查的是勾股定理在实际生活中的运用，解答此类题目的关键是构造出直角三角形，再利用勾股定理解答．
练习册系列答案
名校课堂系列答案
相关题目
如图是一种盛饮料的圆柱形杯，测得其内部底面半径为2.5cm、高为12cm，吸管放进杯里后，外面至少要露出4.6cm，问吸管至少要多长？
一种盛饮料的圆柱形杯，测得内部底面半径为2.5cm，高为12cm，吸管放进杯里（如图），杯口外面至少要露出4.6cm，为节省材料，管长acm的取值范围是
一种盛饮料的圆柱形杯，测得内部底面半径为2.5cm，高为12cm，吸管最大程度倾斜放进杯里，杯口外面至少要露出4.6cm，则吸管至少要
一种盛饮料的圆柱形杯，测得内部底面直径为5cm，高为12cm，吸管放进杯里（如图所示），杯口外面至少要露出4.6cm，问吸管要做多长？