题目内容
两条直线被第三条直线所截，如果同旁内角互补，那么同位角________．
相等
分析：先根据同旁内角互补判定这两条直线平行，再根据两直线平行，同位角相等解答．
解答：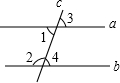
解：如图，∵直线a、b被直线c所截，∠1+∠2=180°，
∴a∥b，
∴∠3=∠4，
即同位角相等．
故答案为：相等．
点评：本题考查了平行线的判定与性质，是基础题，熟记性质与判定是解题的关键，作出图形更形象直观．
分析：先根据同旁内角互补判定这两条直线平行，再根据两直线平行，同位角相等解答．
解答：
解：如图，∵直线a、b被直线c所截，∠1+∠2=180°，∴a∥b，
∴∠3=∠4，
即同位角相等．
故答案为：相等．
点评：本题考查了平行线的判定与性质，是基础题，熟记性质与判定是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
下列语句说法正确的是
| A．两条直线被第三条直线所截，同位角相等 |
| B．如果两个角互为补角，那么其中一定有一个角是钝角 |
| C．过一点有且只有一条直线与已知直线垂直 |
| D．平行于同一直线的两条直线平行 |