题目内容
如图.反比例函数 的图象与直线y=-x-(k+1)相交于点A、C,过点A作x轴的垂线,
的图象与直线y=-x-(k+1)相交于点A、C,过点A作x轴的垂线, 交x轴负半轴于点B,
交x轴负半轴于点B, .
.
(1)求这两个函数的表达式;
(2)求A、C两点的坐标.
解:(1)设点A坐标为(a,b)(a<0,b>0)l分
则S△ABO= OB•AB=
OB•AB= |a|b=-
|a|b=- ab,
ab,
∵S△ABO= ,
,
∴- ab=
ab= ,
,
∴ab=-3.
又∵A(a,b)在 的图象上,
的图象上,
∴ 则k=ab=-3
则k=ab=-3
∴反比例函数的表达式为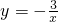
直线的表达式为y=-x+2
(2)解方程组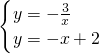
得 ,
,
∴A点坐标为(-1,3),C点坐标(3,-l).
分析:(1)设出点A的坐标,根据所给三角形的面积可得A的横纵坐标的关系,也就求得了反比例函数解析式中的比例系数,可得一次函数解析式;
(2)让一次函数解析式和反比例函数解析式组成方程组求解即可.
点评:考查一次函数和反比例函数的交点问题;根据三角形的面积得到A的横纵坐标的关系是解决本题的突破点.
则S△ABO=
 OB•AB=
OB•AB= |a|b=-
|a|b=- ab,
ab,∵S△ABO=
 ,
,∴-
 ab=
ab= ,
,∴ab=-3.
又∵A(a,b)在
 的图象上,
的图象上,∴
 则k=ab=-3
则k=ab=-3∴反比例函数的表达式为
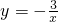
直线的表达式为y=-x+2
(2)解方程组
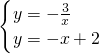
得
 ,
,
∴A点坐标为(-1,3),C点坐标(3,-l).
分析:(1)设出点A的坐标,根据所给三角形的面积可得A的横纵坐标的关系,也就求得了反比例函数解析式中的比例系数,可得一次函数解析式;
(2)让一次函数解析式和反比例函数解析式组成方程组求解即可.
点评:考查一次函数和反比例函数的交点问题;根据三角形的面积得到A的横纵坐标的关系是解决本题的突破点.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
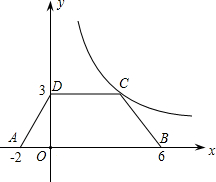 (2012•南昌)如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(2012•南昌)如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C. (2013•和平区一模)如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(2013•和平区一模)如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0). (2012•湖里区一模)如图,反比例函数y=
(2012•湖里区一模)如图,反比例函数y=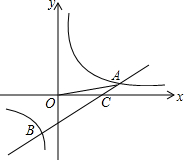 已知:如图,反比例函数的图象和一次函数的图象交于A和B两点,且点A的坐标为(3,1),点B的坐标为(-1,-3),一次函数图象与X轴交于点C.连接OA.
已知:如图,反比例函数的图象和一次函数的图象交于A和B两点,且点A的坐标为(3,1),点B的坐标为(-1,-3),一次函数图象与X轴交于点C.连接OA.