题目内容
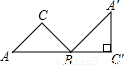
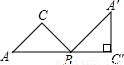
 如图,将腰长为1cm的等腰Rt△ABC绕点B旋转至△A′B′C′的位置,使A、B、C′三点在同一条直线上,则点A经过的最短路线长是( )
如图,将腰长为1cm的等腰Rt△ABC绕点B旋转至△A′B′C′的位置,使A、B、C′三点在同一条直线上,则点A经过的最短路线长是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据题意,点A经过的最短路线长即是以AB为半径,AB=
,以B为圆心的圆中,弧AA′的长度,根据弧长公式可求出.
| 2 |
解答:解:等腰Rt△ABC绕点B旋转至△A′BC′的位置旋转的度数为∠ABA′的度数为135度.
根据弧长公式L=n×
=135×2π×
÷360=
π.
故选B.
根据弧长公式L=n×
| 2πr |
| 360 |
| 2 |
| 3 |
| 4 |
| 2 |
故选B.
点评:解题的关键是求出旋转的角度,利用弧长公式求出其长度.

练习册系列答案
相关题目
 π
π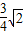 π
π π
π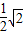 π
π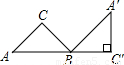
 π
π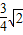 π
π π
π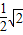 π
π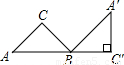
 π
π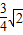 π
π π
π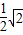 π
π