题目内容
已知在△ABC中,AB=3,AC=2,D在边AB上,∠ACD=∠B,∠BAC的平分线交CD于P、交BC于Q,则 = .
= .
【答案】分析:根据角平分线的定义得∠BAQ=∠CAP,而∠ACD=∠B,根据相似三角形的判定得到△ABQ∽△ACP,由相似三角形的性质得到 ,把AB=3,AC=2代入即可得到答案.
,把AB=3,AC=2代入即可得到答案.
解答:解:∵AQ平分∠BAC,
∴∠BAQ=∠CAP,
而∠ACD=∠B,
∴△ABQ∽△ACP,
∴ ,
,
又∵AB=3,AC=2,
∴ =
= .
.
故答案为 .
.
点评:本题考查了相似三角形的判定与性质:如果两个三角形有两组角对应相等,那么这两个三角形相似;相似三角形的对应边的比相等.也考查了角平分线的定义.
 ,把AB=3,AC=2代入即可得到答案.
,把AB=3,AC=2代入即可得到答案.解答:解:∵AQ平分∠BAC,

∴∠BAQ=∠CAP,
而∠ACD=∠B,
∴△ABQ∽△ACP,
∴
 ,
,又∵AB=3,AC=2,
∴
 =
= .
.故答案为
 .
.点评:本题考查了相似三角形的判定与性质:如果两个三角形有两组角对应相等,那么这两个三角形相似;相似三角形的对应边的比相等.也考查了角平分线的定义.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.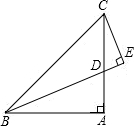 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.