题目内容
(2003•广东)如图,PA和PB分别与⊙O相切于A、B两点,作直径AC,并延长交PB于点D,连接OP,CB.(1)求证:OP∥CB;
(2)若PA=12,DB:DC=2:1,求⊙O的半径.

【答案】分析:(1)PA和PB分别与⊙O相切于A、B两点,则满足切线长定理,易证AB⊥CB,根据AC是直径,可以得到∠ABC=90°,所以OP⊥AB,因而可以得到OP∥CB;
(2)由OP∥CB根据平行线分线段成比例定理,就可以得到 ,再根据PA=PB,从而求出OC即半径的长.
,再根据PA=PB,从而求出OC即半径的长.
解答: (1)证明:连接AB,
(1)证明:连接AB,
∵PA、PB分别与⊙O相切于A、B两点,
∴PA=PB且∠APO=∠BPO.
∴OP⊥AB ①.
∵AC是⊙O的直径,
∴AB⊥CB ②.
由①和②,得:
OP∥CB.
(2)解:∵由(1)知OP∥CB,
∴ .
.
又∵PB=PA=12,
∴ .
.
∴OC=6.
即⊙O的半径为6.
点评:本题主要考查了直径所对的圆周角是直径,以及平行线分线段成比例定理.
(2)由OP∥CB根据平行线分线段成比例定理,就可以得到
 ,再根据PA=PB,从而求出OC即半径的长.
,再根据PA=PB,从而求出OC即半径的长.解答:
 (1)证明:连接AB,
(1)证明:连接AB,∵PA、PB分别与⊙O相切于A、B两点,
∴PA=PB且∠APO=∠BPO.
∴OP⊥AB ①.
∵AC是⊙O的直径,
∴AB⊥CB ②.
由①和②,得:
OP∥CB.
(2)解:∵由(1)知OP∥CB,
∴
 .
.又∵PB=PA=12,

∴
 .
.∴OC=6.
即⊙O的半径为6.
点评:本题主要考查了直径所对的圆周角是直径,以及平行线分线段成比例定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
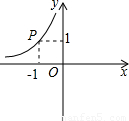
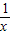 (x>0)
(x>0)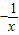 (x>0)
(x>0)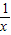 (x<0)
(x<0)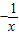 (x<0)
(x<0)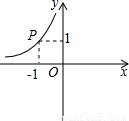
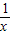 (x>0)
(x>0)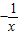 (x>0)
(x>0)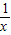 (x<0)
(x<0)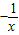 (x<0)
(x<0)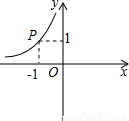
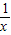 (x>0)
(x>0)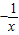 (x>0)
(x>0)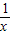 (x<0)
(x<0)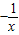 (x<0)
(x<0)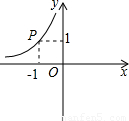
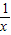 (x>0)
(x>0)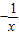 (x>0)
(x>0)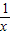 (x<0)
(x<0)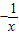 (x<0)
(x<0)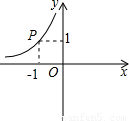
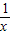 (x>0)
(x>0)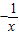 (x>0)
(x>0)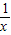 (x<0)
(x<0)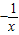 (x<0)
(x<0)