题目内容
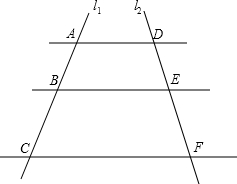 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.
如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.(1)如果AB=6,BC=8,DF=21,求DE的长;
(2)如果DE:DF=2:5,AD=9,CF=14,求BE的长.
分析:(1)根据三条平行线截两条直线,所得的对应线段成比例可得
=
,再由AB=6,BC=8,DF=21即可求出DE的长.
(2)过点D作DG∥AC,交BE于点H,交CF于点G,运用比例关系求出HE及HB的长,然后即可得出BE的长.
| DE |
| DF |
| AB |
| AC |
(2)过点D作DG∥AC,交BE于点H,交CF于点G,运用比例关系求出HE及HB的长,然后即可得出BE的长.
解答: 解:(1)∵AD∥BE∥CF,
解:(1)∵AD∥BE∥CF,
∴
=
,
∵AB=6,BC=8,DF=21,
∴
=
,
∴DE=9.
(2)过点D作DG∥AC,交BE于点H,交CF于点G,
则CG=BH=AD=9,
∴GF=14-9=5,
∵HE∥GF,
∴
=
,
∵DE:DF=2:5,GF=5,
∴
=
,
∴HE=2,
∴BE=9+2=11.
 解:(1)∵AD∥BE∥CF,
解:(1)∵AD∥BE∥CF,∴
| DE |
| DF |
| AB |
| AC |
∵AB=6,BC=8,DF=21,
∴
| DE |
| 21 |
| 6 |
| 6+8 |
∴DE=9.
(2)过点D作DG∥AC,交BE于点H,交CF于点G,
则CG=BH=AD=9,
∴GF=14-9=5,
∵HE∥GF,
∴
| HE |
| GF |
| DE |
| DF |
∵DE:DF=2:5,GF=5,
∴
| HE |
| 5 |
| 2 |
| 5 |
∴HE=2,
∴BE=9+2=11.
点评:本题考查平行线分线段成比例的知识,综合性较强,关键是掌握三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 23、如图,已知AD∥BE,∠CDE=∠C,试说明∠A=∠E的理由.
23、如图,已知AD∥BE,∠CDE=∠C,试说明∠A=∠E的理由. 如图,已知AD∥BE∥CF,BC=3,DE:EF=2:1,则AC=
如图,已知AD∥BE∥CF,BC=3,DE:EF=2:1,则AC= 如图,已知AD⊥BE,垂足C是BE的中点,AB=DE.求证:AB∥DE.
如图,已知AD⊥BE,垂足C是BE的中点,AB=DE.求证:AB∥DE. 填写理由或步骤
填写理由或步骤