��Ŀ����
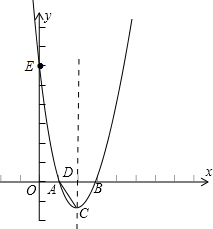
��ͼ1��������y=ax2-10ax+8��x�ύ��A��C���㣬��y �ύ�ڵ�B����C�������Ϊ��2��0����1���������ߵĺ�������ʽ��A��B��������ꣻ
��2����ͼ�����D���߶�OA�ϵ�һ�����㣬����D��DE��x�ύAB�ڵ�E������E��EF��y�ᣬ����ΪF����OD=x������ODEF�����ΪS����S��x֮��ĺ�����ϵʽ�������S�����ֵ����ʱ��D�����ꣻ
��3���������ߵĶԳ�����AB���ڵ�P����ͼ2������Q���������ϵ�һ�����㣬��R��x���ϵ�һ�����㣮���������P��Q��R��AΪ������ı�����ƽ���ı���ʱ����Q�����꣮

��������1�����������öԳ���ķ��̣�����AB��x�ᣬ��϶Գ�������ʣ��ɵ�AB=10������Rt��AOC�У��ɹ��ɶ����ô𰸣�
��2���������⽫��PAC���ܳ���PC+PA��ʾ�������������ߵĶԳ��Է����ɵ�P��ΪBCֱ��x=5�Ľ��㣻�ɴ���BC�Ľ���ʽΪ��y=kx+b����A��8��0����B��0��8������ɵ�k��b��ֵ�������ɵ������ʽ��
��3��������ڣ���Rt��MOC��Rt��PBE�У����ݹ��ɶ��������MP��BC�����ɵô𰸣�
��2���������⽫��PAC���ܳ���PC+PA��ʾ�������������ߵĶԳ��Է����ɵ�P��ΪBCֱ��x=5�Ľ��㣻�ɴ���BC�Ľ���ʽΪ��y=kx+b����A��8��0����B��0��8������ɵ�k��b��ֵ�������ɵ������ʽ��
��3��������ڣ���Rt��MOC��Rt��PBE�У����ݹ��ɶ��������MP��BC�����ɵô𰸣�
����⣺��1����y=ax2-10ax+8��
�������ߵĶԳ���Ϊ��x=-
=-
=5��
��x=0���õ�y=8��
���B��������0��8����
�ߵ�C����Ϊ����2��0����
�ߵ�A���C���ڶԳ���x=5�Գƣ�
���A��������8��0����
��C��2��0������y=ax2-10ax+8�ã�4a-20a+8=0��
��a=
��
�������ߵĺ�������ʽΪy=
x2-5x+8��
��2����A��8��0����B��0��8����
����ֱ��AB�Ľ���ʽΪy=kx+b��
��A��B�������ã�
'
��ã�
��
��ֱ��AB����ʽΪy=-x+8��
��OD=x����E������Ϊx��
����ֱ��AB����ʽ�ã�y=-x+8����ED=-x+8��
�������S=x��-x+8��=-x2+8x��0��x��8��
��x=-
=4����D��4��0��ʱ��S�����ֵ�����ֵΪ16��
��3���������⻭��ͼ�Σ���ͼ��ʾ��

���ڷ��������ĵ�Q��R��ʹ��P��R��Q��AΪ������ı���Ϊƽ���ı��Σ�
��Q�ڶԳ����ұߣ���x=5����ֱ��AB����ʽ�����y=3����Q������Ϊ3��
��y=3���������߽���ʽ�ã�3=
x2-5x+8 ��ã�x=5��
��
��Q��������Ϊ-3�����е㣨5��
��-3��
�� Q����������5+
��3����5-
��3����5+
��-3����5-
��-3����
�������ߵĶԳ���Ϊ��x=-
| b |
| 2a |
| -10a |
| 2a |
��x=0���õ�y=8��
���B��������0��8����
�ߵ�C����Ϊ����2��0����
�ߵ�A���C���ڶԳ���x=5�Գƣ�
���A��������8��0����
��C��2��0������y=ax2-10ax+8�ã�4a-20a+8=0��
��a=
| 1 |
| 2 |
�������ߵĺ�������ʽΪy=
| 1 |
| 2 |
��2����A��8��0����B��0��8����
����ֱ��AB�Ľ���ʽΪy=kx+b��
��A��B�������ã�
|
��ã�
|
��ֱ��AB����ʽΪy=-x+8��
��OD=x����E������Ϊx��
����ֱ��AB����ʽ�ã�y=-x+8����ED=-x+8��
�������S=x��-x+8��=-x2+8x��0��x��8��
��x=-
| b |
| 2a |
��3���������⻭��ͼ�Σ���ͼ��ʾ��

���ڷ��������ĵ�Q��R��ʹ��P��R��Q��AΪ������ı���Ϊƽ���ı��Σ�
��Q�ڶԳ����ұߣ���x=5����ֱ��AB����ʽ�����y=3����Q������Ϊ3��
��y=3���������߽���ʽ�ã�3=
| 1 |
| 2 |
| 15 |
��Q��������Ϊ-3�����е㣨5��
| 3 |
�� Q����������5+
| 15 |
| 15 |
| 3 |
| 3 |
���������⿼���˶��κ������ۺ����ã������κ�����ͼ�������ʽ���ϴ��������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
�����Ŀ
 ��֪���κ�����ͼ���Ǿ�����A��1��0����B��3��0����E��0��6�������һ�������ߣ�
��֪���κ�����ͼ���Ǿ�����A��1��0����B��3��0����E��0��6�������һ�������ߣ� �Ķ����ϣ���ͼ1������ABC����������ֱ�������ˮƽ�ߴ�ֱ������ֱ�ߣ��������ֱ��֮��ľ���С�ABC�ġ�ˮƽ������a�����м������ֱ���ڡ�ABC�ڲ��߶εij��ȽС�ABC�ġ�Ǧ���ߡ���h�������ǿɵó�һ�ּ���������������·�����S��ABC=
�Ķ����ϣ���ͼ1������ABC����������ֱ�������ˮƽ�ߴ�ֱ������ֱ�ߣ��������ֱ��֮��ľ���С�ABC�ġ�ˮƽ������a�����м������ֱ���ڡ�ABC�ڲ��߶εij��ȽС�ABC�ġ�Ǧ���ߡ���h�������ǿɵó�һ�ּ���������������·�����S��ABC=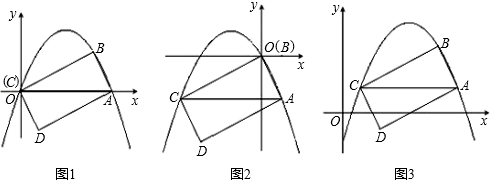
 ��ͼ����������
��ͼ����������