题目内容
 如图,点D、E在BC上,AB=AC,BD=EC,要证∠1=∠2,可以先由AB=AC,得∠B=________;再证△ABD≌________,得∠1=∠2.
如图,点D、E在BC上,AB=AC,BD=EC,要证∠1=∠2,可以先由AB=AC,得∠B=________;再证△ABD≌________,得∠1=∠2.
∠C △ACE
分析:由AB=AC,根据等边对等角,得到∠B=∠C,然后再由AB=AC,BD=EC,利用“SAS”得到△ABD和△ACE全等,根据全等三角形的性质得到对应角∠1和∠2相等.
解答:证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
AB=AC,∠B=∠C,BD=CE,
∴△ABD≌△ACE,
∴∠1=∠2.
故答案为:∠C;△ACE
点评:此题考查了全等三角形的性质与判断,考查了学生分析问题,解决问题的能力.根据图形,选择合适的证明全等方法是解题的关键.其中全等三角形的性质为全等三角形的对应边相等,对应角也相等.全等三角形的判断方法有:SAS;ASA;SSS;AAS以及HL(直角三角形全等的方法).
分析:由AB=AC,根据等边对等角,得到∠B=∠C,然后再由AB=AC,BD=EC,利用“SAS”得到△ABD和△ACE全等,根据全等三角形的性质得到对应角∠1和∠2相等.
解答:证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
AB=AC,∠B=∠C,BD=CE,
∴△ABD≌△ACE,
∴∠1=∠2.
故答案为:∠C;△ACE
点评:此题考查了全等三角形的性质与判断,考查了学生分析问题,解决问题的能力.根据图形,选择合适的证明全等方法是解题的关键.其中全等三角形的性质为全等三角形的对应边相等,对应角也相等.全等三角形的判断方法有:SAS;ASA;SSS;AAS以及HL(直角三角形全等的方法).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
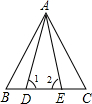 已知:如图,点D、E在BC上,BD=EC,∠1=∠2,求证:AB=AC.
已知:如图,点D、E在BC上,BD=EC,∠1=∠2,求证:AB=AC. 如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:AB=DC.
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:AB=DC. 如图,点E、F在BC上,∠B=∠C,AB=DC,且BE=CF.
如图,点E、F在BC上,∠B=∠C,AB=DC,且BE=CF.
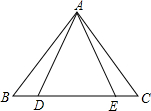 如图,点D、E在BC上,AB=AC,AD=AE.BD和CE有怎样的关系?请说明理由.
如图,点D、E在BC上,AB=AC,AD=AE.BD和CE有怎样的关系?请说明理由.