题目内容
【题目】如图1,抛物线![]() :
:![]() 与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线
与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线![]() 的顶点为G.
的顶点为G.
(1)求出抛物线![]() 的解析式,并写出点G的坐标;
的解析式,并写出点G的坐标;
(2)如图2,将抛物线![]() 向下平移k(k>0)个单位,得到抛物线
向下平移k(k>0)个单位,得到抛物线![]() ,设
,设![]() 与x轴的交点为
与x轴的交点为![]() 、
、![]() ,顶点为
,顶点为![]() ,当△
,当△![]() 是等边三角形时,求k的值:
是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点(介于O与B之间),过点M作x轴的垂线分别交抛物线![]() 、
、![]() 于P、Q两点,是否存在M点,使得以A、Q、M为顶点的三角形与以P、M、B为顶点的三角形相似,若存在,求出点M的坐标:若不存在,请说明理由.
于P、Q两点,是否存在M点,使得以A、Q、M为顶点的三角形与以P、M、B为顶点的三角形相似,若存在,求出点M的坐标:若不存在,请说明理由.
【答案】(1)![]() , G的坐标为(1,4)(2)k=1;(3)M点的坐标为
, G的坐标为(1,4)(2)k=1;(3)M点的坐标为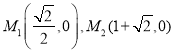
【解析】
(1)由点A的坐标及OC=3OA得点C坐标,将A、C坐标代入解析式求解可得;
(2)设抛物线C2的解析式为y=-x2+2x+3-k,即y=-(x-1)2+4-k,′作G′D⊥x轴于点D,设B′D=m,由等边三角形性质知点B′的坐标为(m+1,0),点G′的坐标为(1,![]() m),代入所设解析式求解可得;
m),代入所设解析式求解可得;
(3)设M(a,0),则P(a,-a2+2a+3)、Q(a,-a2+2a+2),分别用含a的式子表示AM,BM,PM,QM.再由题意分两种情况相似:①△AMQ∽△BMP,②△AMQ∽△PMB.根据对应边成比例建立关于a的方程,解之求得a的值从而进一步求解.
解:(1)∵点A的坐标为(﹣1,0),
∴OA=1,
∴OC=3OA,
∴点C的坐标为(0,3),
将A、C坐标代入![]() ,得:
,得:
![]()
解得:![]() ,
,
∴抛物线C1的解析式为![]() ,
,
所以点G的坐标为(1,4).
(2)设抛物线C2的解析式为![]() ,即
,即![]() ,
,
过点G′作![]() 轴于点D,设
轴于点D,设![]() ,
,
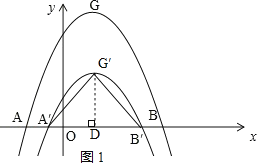
∵△![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
则点![]() 的坐标为(m+1,0),点
的坐标为(m+1,0),点![]() 的坐标为(1,
的坐标为(1,![]() m),
m),
将点![]() 、
、![]() 的坐标代入
的坐标代入![]() ,得:
,得:
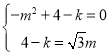 ,
,
解得: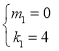 (舍去)
(舍去)
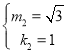
∴k=1;
(3)设M(![]() ,0),则
,0),则![]() ,
,
∵M介于O与B之间,∴![]()
∵A(-1,0),B(3,0)
![]()
![]()
分两种情况:
当△AMQ∽△BMP时,有![]() ,可得
,可得
![]()
![]()
![]()
![]() (舍去)
(舍去)
∴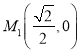
②当△AMQ∽△PMB时,有![]() ,可得
,可得
![]()
整理得![]()
![]()
解得:![]()
![]()
∴![]()
综上所述M点的坐标为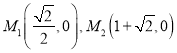

 阅读快车系列答案
阅读快车系列答案