Question

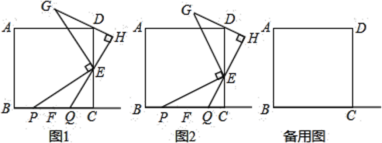
【题目】在△ABC中，∠ACB=90°，AC=BC，P是△ABC内一点，且满足PA=3，PB=1，PC=2，则∠BPC的度数为___________．

Answer 1

【答案】135°

【解析】

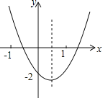
过点C作CD⊥CP，使CD=CP=2，连接CD，PD，AD，根据AC=BC，由同角的余角相等得到夹角相等，利用SAS的三角形ACD与三角形CBP全等，利用全等三角形对应边相等，对应角相等得到AD=BP=1，∠ADC=∠BPC，在直角三角形DCP中，利用勾股定理求出DP的长，由AD以及AP的长，利用勾股定理的逆定理得到三角形ADP为直角三角形，由∠4+∠5求出∠ADC度数，即为∠BPC度数．

过点C作CD⊥CP，使CD=CP=2，连接CD，PD，AD，

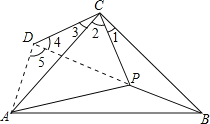
∵∠1+∠2=∠ACB=90°=∠DCP=∠3+∠2，
∴∠1=∠3，
在△CAD和△CBP中，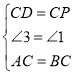

∴△CAD≌△CBP（SAS），

∴DA=PB=1，∠ADC=∠BPC，
在等腰Rt△DCP中，∠4=45°，
根据勾股定理得：DP2=CD2+CP2=22+22=8，
∵DP2+DA2=8+1=9，AP2=32=9，
∴DP2+DA2=AP2，
∴△ADP为直角三角形，即∠5=90°，
则∠BPC=∠ADC=∠4+∠5=45°+90°=135°．