题目内容
如图:正方形ABCO的边长为3,过A(0,3)点作直线AD交x轴于D点,且D点的坐标为(4,0),线段AD上有一动点,以每秒一个单位长度的速度移动.
(1)求直线AD的解析式;
(2)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P,求经过B、O、P三点的抛物线的解析式;
(3)若动点从A点开始沿AD方向运动到达的位置为点P1,过P1作P1E⊥x轴,垂足为E,设四边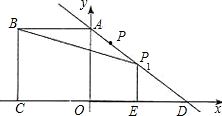 形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
(1)求直线AD的解析式;
(2)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P,求经过B、O、P三点的抛物线的解析式;
(3)若动点从A点开始沿AD方向运动到达的位置为点P1,过P1作P1E⊥x轴,垂足为E,设四边
 形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.(1)设直线AD的解析式为y=kx+b(k≠0),
则
,
解得
.
解析式为:y=-
x+3.
(2)因为AP=2.5,AD=5,
所以P(2,1.5),
设过B,O,P的抛物线为y=ax2+bx+c(a≠0),
将B(-3,3),O(0,0),P(2,1.5),
则
,
解得
,
解析式为y=
x2+
x.
(3)设P(x,y),
则y=-
x+3
S=
(y+3)×(3+x)
即S=-
x2+
x+9
所以P1(
,
)时,S最大=
.

则
|
解得
|
解析式为:y=-
| 3 |
| 4 |
(2)因为AP=2.5,AD=5,
所以P(2,1.5),
设过B,O,P的抛物线为y=ax2+bx+c(a≠0),
将B(-3,3),O(0,0),P(2,1.5),
则
|
解得
|
解析式为y=
| 7 |
| 20 |
| 1 |
| 20 |
(3)设P(x,y),
则y=-
| 3 |
| 4 |
S=
| 1 |
| 2 |
即S=-
| 3 |
| 8 |
| 15 |
| 8 |
所以P1(
| 5 |
| 2 |
| 9 |
| 8 |
| 363 |
| 32 |


练习册系列答案
相关题目

 的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.
的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.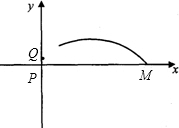
 的长是方程x2-6x+5=0的两个实数根.
的长是方程x2-6x+5=0的两个实数根.
