Question

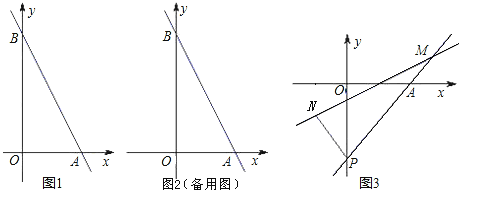
【题目】如图1，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（2，0）, B（0，4）.

（1）求直线AB的解析式；

（2）若点M为直线y=mx在第一象限上一点，且△ABM是等腰直角三角形，求m的值．

（3）如图3，过点A（2，0）的直线交y轴负半轴于点P，N点的横坐标为-1，过N点的直线交AP于点M.求的值.

Answer 1

【答案】（1）y=﹣2x+4；（2）m的值是或或1；（3）2.

【解析】

（1）设直线AB的解析式是y=kx+b，代入得到方程组，求出即可；

（2）当BM⊥BA，且BM=BA时，过M作MN⊥y轴于N，证△BMN≌△ABO（AAS），求出M的坐标即可；②当AM⊥BA，且AM=BA时，过M作MN⊥x轴于N，同法求出M的坐标；③当AM⊥BM，且AM=BM时，过M作MN⊥x轴于N，MH⊥y轴于H，证△BHM≌△AMN，求出M的坐标即可．

（3）设NM与x轴的交点为H，分别过M、H作x轴的垂线垂足为G，HD交MP于D点，求出H、G的坐标，证△AMG≌△ADH，△AMG≌△ADH≌△DPC≌△NPC，推出PN=PD=AD=AM代入即可求出答案．

（1） ∵A（2，0），B（0，4），

设直线AB的解析式是y=kx+b，

代入得：，

解得：k=﹣2，b=4，

∴直线AB的解析式是y=﹣2x+4．

（2）如图，分三种情况：

①如图①，当BM⊥BA，且BM=BA时，过M作MN⊥y轴于N，

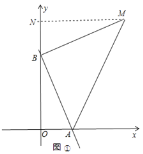
∵BM⊥BA，MN⊥y轴，OB⊥OA，

∴∠MBA=∠MNB=∠BOA=90°，

∴∠NBM+∠NMB=90°，∠ABO+∠NBM=90°，

∴∠ABO=∠NMB，

在△BMN和△ABO中

，

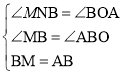∴△BMN≌△ABO（AAS），

MN=OB=4，BN=OA=2，

∴ON=2+4=6，

∴M的坐标为（4，6 ），

代入y=mx得：m=，

②如图②，当AM⊥BA，且AM=BA时，过M作MN⊥x轴于N，

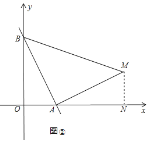
易知△BOA≌△ANM（AAS），

同理求出M的坐标为（6，2），

代入y=mx得：m=，

③如图③，

当AM⊥BM，且AM=BM时，过M作MN⊥X轴于N，MH⊥Y轴于H，

∴四边形ONMH为矩形，

易知△BHM≌△AMN，

∴MN=MH，

设M（x1，x1）代入y=mx得：x1=m x1，

∴，

答：m的值是或或1．

（3）如图3，设NM与x轴的交点为H，过M作MG⊥x轴于G，过H作HD⊥x轴，

HD交MP于D点，

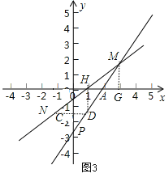
即：∠MGA=∠DHA=900，连接ND，ND 交y轴于C点

由与x轴交于H点，∴H（1，0），

由与y=kx﹣2k交于M点，∴M（3，k），

而A（2，0），

∴A为HG的中点，AG=AH，∠MAG=∠DAH

∴△AMG≌△ADH（ASA），∴AM=AD

又因为N点的横坐标为﹣1，且在上，

∴N（-1，﹣k），同理D（1，﹣k）

∴N关于y轴对称点为D

∴PC是ND的垂直平分线∴PN=PD, CD=NC=HA=1，∠DCP=∠DHA=900，ND平行于X轴

∴∠CDP=∠HAD

∴△ADH≌△DPC ∴AD= PD

∴PN=PD=AD=AM，

∴．