题目内容
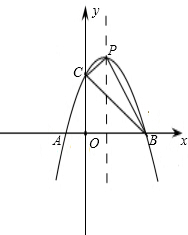
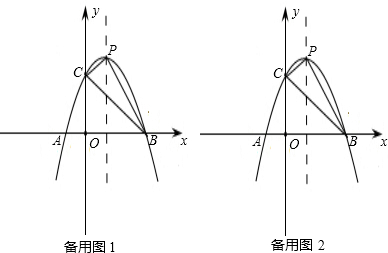
如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.
(1)求抛物线的对称轴和点B的坐标;
(2)过点C作CP⊥对称轴于点P,连接BC交对称轴于点D,连接AC、BP,且∠BPD=∠BCP,求抛物线的解析式;
(3)在(2)的条件下,设抛物线的顶点为G,连接BG、CG、求△BCG的面积.
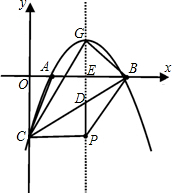
(1)求抛物线的对称轴和点B的坐标;
(2)过点C作CP⊥对称轴于点P,连接BC交对称轴于点D,连接AC、BP,且∠BPD=∠BCP,求抛物线的解析式;
(3)在(2)的条件下,设抛物线的顶点为G,连接BG、CG、求△BCG的面积.

(1)对称轴是x=-
=-
=2,…(2分)
∵点A(1,0)且点A、B关于x=2对称,
∴点B(3,0);…(4分)
(2)点A(1,0),B(3,0),
∴AB=2,
∵CP⊥对称轴于P,
∴CP∥AB,
∵对称轴是x=2,
∴AB∥CP且AB=CP,
∴四边形ABPC是平行四边形,…(5分)
设点C(0,x)(x<0),
在Rt△AOC中,AC=
,
∴BP=
,
在Rt△BOC中,BC=
,
∵
=
=
,
∴BD=
,
∵∠BPD=∠BCP且∠PBD=∠CBP,
∴△BPD∽△BCP,…(7分)
∴BP2=BD•BC,
即(
)2=
•
,
∴x2+1=
(x2+9),
∴x1=
,x2=-
,
∵点C在y轴的负半轴上,
∴点C(0,-
),…(8分)
∴y=ax2-4ax-
,
∵过点(1,0),
∴a-4a-
=0,
解得:a=-
.
∴解析式是:y=-
x2+
x-
;…(9分)
(3)当x=2时,y=
,
顶点坐标G是(2,
),…(10分)
设CG的解析式是:y=kx+b,
∵过点(0,-
)(2,
),
∴
,
∴y=
x-
,…(11分)
设CG与x轴的交点为H,
令y=0,则
x-
=0,
得x=
,
即H(
,0),…(11分)
∴BH=3-
=
,
∴S△BCG=S△BHG+S△BHC=
×
×
+
×
×|-
|=
+
=
…(13分)
| b |
| 2a |
| -4a |
| 2a |
∵点A(1,0)且点A、B关于x=2对称,
∴点B(3,0);…(4分)
(2)点A(1,0),B(3,0),
∴AB=2,
∵CP⊥对称轴于P,
∴CP∥AB,
∵对称轴是x=2,
∴AB∥CP且AB=CP,
∴四边形ABPC是平行四边形,…(5分)
设点C(0,x)(x<0),
在Rt△AOC中,AC=
| x2+1 |
∴BP=
| x2+1 |
在Rt△BOC中,BC=
| x2+9 |
∵
| BD |
| BC |
| BE |
| BO |
| 1 |
| 3 |
∴BD=
| 1 |
| 3 |
| x2+9 |
∵∠BPD=∠BCP且∠PBD=∠CBP,
∴△BPD∽△BCP,…(7分)
∴BP2=BD•BC,
即(
| x2+1 |
| 1 |
| 3 |
| x2+9 |
| x2+9 |
∴x2+1=
| 1 |
| 3 |
∴x1=
| 3 |
| 3 |
∵点C在y轴的负半轴上,
∴点C(0,-
| 3 |
∴y=ax2-4ax-
| 3 |
∵过点(1,0),
∴a-4a-
| 3 |
解得:a=-
| ||
| 3 |
∴解析式是:y=-
| ||
| 3 |
4
| ||
| 3 |
| 3 |
(3)当x=2时,y=
| ||
| 3 |

顶点坐标G是(2,
| ||
| 3 |
设CG的解析式是:y=kx+b,
∵过点(0,-
| 3 |
| ||
| 3 |
∴
|
∴y=
2
| ||
| 3 |
| 3 |
设CG与x轴的交点为H,
令y=0,则
2
| ||
| 3 |
| 3 |
得x=
| 3 |
| 2 |
即H(
| 3 |
| 2 |
∴BH=3-
| 3 |
| 2 |
| 3 |
| 2 |
∴S△BCG=S△BHG+S△BHC=
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 4 |
3
| ||
| 4 |
| 3 |

练习册系列答案
相关题目
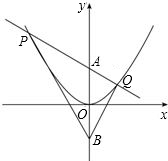 于P,Q两点.
于P,Q两点.
 三点.
三点. 得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).
得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).