题目内容
将一根长为16 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为 和
和 .
.
(1)求 与
与 的关系式,并写出
的关系式,并写出 的取值范围;
的取值范围;
(2)将两圆的面积和S表示成 的函数关系式,求S的最小值.
的函数关系式,求S的最小值.
 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为 和
和 .
. (1)求
 与
与 的关系式,并写出
的关系式,并写出 的取值范围;
的取值范围;(2)将两圆的面积和S表示成
 的函数关系式,求S的最小值.
的函数关系式,求S的最小值.(1)0<r1<8(2)32π
解:(1)由题意,有2πr1+2πr2=16π,则r1+r2=8。
∵r1>0,r2>0,∴0<r1<8。
∴r1与r2的关系式为r1+r2=8,r1的取值范围是0<r1<8厘米。
(2)∵r1+r2=8,∴r2=8﹣r1。
又∵ ,
,
∴当r1=4厘米时,S有最小值32π平方厘米。
(1)由圆的周长公式表示出半径分别为r1和r2的圆的周长,再根据这两个圆的周长之和等于16π厘米列出关系式即可。
(2)先由(1)可得r2=8﹣r1,再根据圆的面积公式即可得到两圆的面积和S表示成r1的函数关系式,然后根据函数的性质即可求出S的最小值。
∵r1>0,r2>0,∴0<r1<8。
∴r1与r2的关系式为r1+r2=8,r1的取值范围是0<r1<8厘米。
(2)∵r1+r2=8,∴r2=8﹣r1。
又∵
 ,
,∴当r1=4厘米时,S有最小值32π平方厘米。
(1)由圆的周长公式表示出半径分别为r1和r2的圆的周长,再根据这两个圆的周长之和等于16π厘米列出关系式即可。
(2)先由(1)可得r2=8﹣r1,再根据圆的面积公式即可得到两圆的面积和S表示成r1的函数关系式,然后根据函数的性质即可求出S的最小值。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 ,求点B的坐标。
,求点B的坐标。

 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
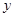 元,镜子的宽是
元,镜子的宽是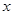 米.
米. 与y轴的交点坐标是( )
与y轴的交点坐标是( ) 是( )
是( ) 与
与 轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则
轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则

 (填“
(填“ ”或“
”或“ ”);
”);