题目内容
【题目】如图,![]() 内接于
内接于![]() ,且
,且![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.

![]() 试判断
试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求阴影的面积.
,求阴影的面积.
【答案】(1)相切,理由见解析;(2)![]() .
.
【解析】
(1)根据等腰三角形性质求出∠FBA=∠EBA=∠C,推出∠D=∠C=∠FBA,根据∠DAB=90°推出∠D+∠DBA=90°,求出∠ABD+∠FBA=90°,根据切线的判定推出即可.
(2)连接OA,求出∠BOA=60°,求出AB长,求出BD、AD,求出OB,根据三角形的面积求出△ABD面积,即可求出△BAO面积,求出扇形BOA面积,即可求出答案.
![]() 解:
解:![]() 与
与![]() 的位置关系是相切,
的位置关系是相切,
理由是:∵![]() 和
和![]() 都对弧
都对弧![]() ,
,
∴![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() (已证),
(已证),
∴![]() ,
,
∴![]() ,
,
∵![]() 是半径,
是半径,
∴![]() 是
是![]() 的切线,
的切线,
即![]() 与
与![]() 的位置关系是相切;
的位置关系是相切;
![]() 连接
连接![]() ,
,
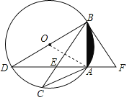
∵![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
由勾股定理得![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
又∵![]() ,
,
∴根据等底同高的三角形的面积相等得出![]() ,
,
![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目