题目内容
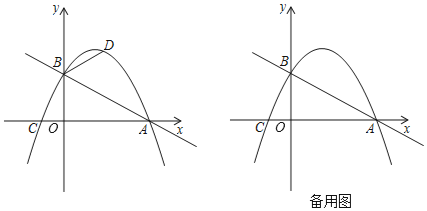
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点
与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与x轴的负半轴交于点
两点且与x轴的负半轴交于点![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 已知
已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当
和抛物线上的动点,当![]() 为顶点的四边形是平行四边形时,直接写出所有符合条件的
为顶点的四边形是平行四边形时,直接写出所有符合条件的![]() 点的坐标.
点的坐标.
【答案】(1)![]() (2)点
(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
![]() 求得
求得![]() 两点坐标,代入抛物线解析式,获得
两点坐标,代入抛物线解析式,获得![]() 的值,获得抛物线的解析式.
的值,获得抛物线的解析式.
![]() 通过平行线分割
通过平行线分割![]() 倍角条件,得到相等的角关系,利用等角的三角函数值相等,得到点坐标.
倍角条件,得到相等的角关系,利用等角的三角函数值相等,得到点坐标.
![]() 四点作平行四边形,以已知线段
四点作平行四边形,以已知线段![]() 为边和对角线分类讨论,当
为边和对角线分类讨论,当![]() 为边时,以
为边时,以![]() 的关系建立方程求解,当
的关系建立方程求解,当![]() 为对角线时,
为对角线时,![]() 与
与![]() 互相平分,利用直线相交获得点
互相平分,利用直线相交获得点![]() 坐标.
坐标.
![]() 在
在![]() 中,令
中,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]()
![]()
把![]() ,代入
,代入![]() ,得
,得
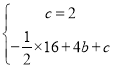 ,解得
,解得![]()
![]() 抛物线得解析式为
抛物线得解析式为![]()
![]() 如图,过点
如图,过点![]() 作
作![]() 轴得平行线交抛物线于点
轴得平行线交抛物线于点![]() ,过点
,过点![]() 作
作![]() 得垂线,垂足为
得垂线,垂足为![]()
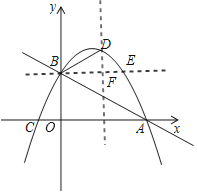
![]() 轴,
轴,
![]()
![]()
![]()
即![]()
![]()
![]()
设![]() 点的坐标为
点的坐标为 ![]() ,则
,则![]()
![]() ,
,![]()
![]() ,即
,即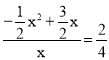
解得![]() (舍去),
(舍去),![]()
当![]() 时,
时,![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]() 当
当![]() 为边时,
为边时, ![]()
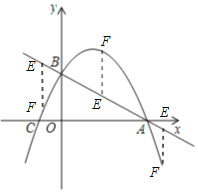
设 ![]()
![]()
解得 ![]()
当![]() 为对角线时,
为对角线时,![]() 与
与![]() 互相平分
互相平分
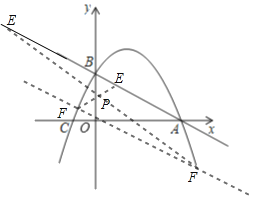
过点![]() 作
作![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() ,
,![]()
求得直线![]() 解析式为
解析式为![]()
直线![]() 与
与![]() 的交点为
的交点为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() 或
或![]()
![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
拼单数x(单位:单) | 2 | 4 | 8 | 12 |
单价y(单位:元) | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m(单位:件) | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题:
(1)请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;
(2)拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?
(3)在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?