题目内容

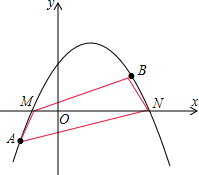
已知抛物线y=ax²+bx+c（a≠0）经过A（-2，-3）、B（3，2）两点，且与x轴相交于M、N两点，当以线段MN为直径的圆的面积最小时，求M、N两点的坐标和四边形AMBN的面积．

解：由抛物线经过A（-2，-3）、B（3，2）两点可得b=1-a，c=-（1+6a）
∴MN=丨x₁-x₂丨=| $\text{[math]}$ |=|± $\text{[math]}$ |= $\text{[math]}$ = $\text{[math]}$ ．
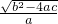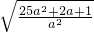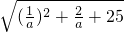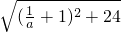当a=-1时，MN_最小=2 $\text{[math]}$
此时，b=2，c=5，
∴函数的解析式为：y=-x²+2x+5．
∴M（1- $\text{[math]}$ ，0），N（1+ $\text{[math]}$ ，0），
此时，四边形AMBN的面积S= $\text{[math]}$ MN•（|y_A|+|y_B|）= $\text{[math]}$ ×2 $\text{[math]}$ ×（3+2）=5 $\text{[math]}$ ．
分析：将点A、B的坐标分别代入已知函数解析式，即可求得以a表示的b、c的值；然后由两点间的距离公式求得MN= 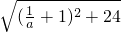$\text{[math]}$ ，由二次函数的最值求得：
当a=-1时，MN_最小=2 $\text{[math]}$ ．从而易求点M、N的坐标；最后根据四边形的面积=两个三角形的面积之和来求四边形AMBN的面积．
点评：本题考查了二次函数综合题．其中涉及到的知识点有：待定系数法求二次函数的解析式，根与系数的关系与代数式的变形，二次函数最值的求法以及三角形面积的计算．在求四边形AMBN的面积时，采用了“分割法”．