题目内容
 如图,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于G点,下列结论中:
如图,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于G点,下列结论中:
①EF⊥AC;②四边形ADFE是菱形; ③AD=4AG;④△DBF≌△EFA.正确的结论是
- A.②④
- B.①③
- C.②③④
- D.①③④
D
分析:运用等边三角形的性质,平行四边形的判定,三角形的全等即可解出本题.
解答: 解:(1)如图,连接CF,∠ABC=60°.△ABC是直角三角形,
解:(1)如图,连接CF,∠ABC=60°.△ABC是直角三角形,
所以CF= AB=AF,
AB=AF,
△ACE是等边三角形,
所以AE=CE,而△AEF与△CEF共一条边,由此可知,△AEF≌△CEF.
所以A点和C点是关于EF的对称点,EF⊥AC成立;
(2)F是AB中点,所以DF⊥AB,那么在△ADF中AD是斜边,DF是直角边,
即AD>DF,由此可知四边形ADFE不可能是菱形.
(3)∠DAB=∠ABC=60°,所以AD∥BC.AC⊥EF,∠ACB=90°,所以EF∥AD.由上可知AD∥EF.
EF=2AF=AD.
故AD=EF.
四边形ADFE是平行四边形,AG= AF=
AF= AB=
AB= AD,
AD,
即AD=4AG.
(4)由四边形ADFE是平行四边形可得AE=DF,AD=FE,而AD=DB,
所以DB=FE,AF=FB,
故得△DBF≌△EFA.
点评:本题综合运用等边三角形的性质,三角形的全等,直角三角形的中线以及平行四边形的判定.
分析:运用等边三角形的性质,平行四边形的判定,三角形的全等即可解出本题.
解答:
 解:(1)如图,连接CF,∠ABC=60°.△ABC是直角三角形,
解:(1)如图,连接CF,∠ABC=60°.△ABC是直角三角形,所以CF=
 AB=AF,
AB=AF,△ACE是等边三角形,
所以AE=CE,而△AEF与△CEF共一条边,由此可知,△AEF≌△CEF.
所以A点和C点是关于EF的对称点,EF⊥AC成立;
(2)F是AB中点,所以DF⊥AB,那么在△ADF中AD是斜边,DF是直角边,
即AD>DF,由此可知四边形ADFE不可能是菱形.
(3)∠DAB=∠ABC=60°,所以AD∥BC.AC⊥EF,∠ACB=90°,所以EF∥AD.由上可知AD∥EF.
EF=2AF=AD.
故AD=EF.
四边形ADFE是平行四边形,AG=
 AF=
AF= AB=
AB= AD,
AD,即AD=4AG.
(4)由四边形ADFE是平行四边形可得AE=DF,AD=FE,而AD=DB,
所以DB=FE,AF=FB,
故得△DBF≌△EFA.
点评:本题综合运用等边三角形的性质,三角形的全等,直角三角形的中线以及平行四边形的判定.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
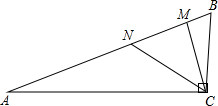 如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是
如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是 10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( )
10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( ) 如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( ) 如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE.
如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE. 如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.
如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.